无题

title: JJ的算法之旅
date: 2023-09-17 01:39:06
descriptions: 记录日常算法学习和机试刷题笔记
tags:

kk=kk&(kk-1)，可以消除kk二进制的最后一个1

1
#include<bits/stdc++.h>

参考

https://labuladong.gitee.io/algo/home/

1
2
3
# 找到数组中的最大值及其索引 速度更快
    max_num = max(nums)
    max_idx = nums.index(max_num)
  • Floyd
  • 背包问题 天平称0
  • 手写数据结构代码，链表、二叉树 P8744 [蓝桥杯 2021 省 A] 左孩子右兄弟
  • dfs,bfs
  • 前缀和、二分、差分
  • 刷动态规划
  • 时间复杂度控制在10^7

image-20240412104816902

基础知识

模板

输入输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 输入样例
# 3 2 1 6 0 5
nums = list(map(int, input().split()))

# 输入样例
# 3
# 1 2 4 
Len = int(input())
nums = list(map(int, input().split()))

# 第一行输入两个整数，第一个代表数组的长度，第二个代表k，数字与数字之间用空格间开
# 第二行输入一行数字代表数组arr。数字与数字之间用空格间开
# 输入样例
# 3 2
# 3 2 1
n, k = map(int, input().split())  # 注意这个输入是按行的，分割
nums = list(map(int, input().split()))

构造

构建二维数组大坑！

1
2
np.zeros((m, n)) √
dp=[([0]*(n+1))]*(n+1) × 引用方式修改，每一列的第i都会跟着bian

类初始化

1
2
3
4
5
6
7
8
9
10
11
12
class Cstudent
{
public:
	Cstudent(string string1,string string2,int t):name(string1), school(string2), tele(t){}
	void set_data();
	void show_data();
private:
	string name;
	string school;
	int tele;
};

字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 大小写转换
## 函数法
msg='www.BAIDU.com.123'
print(msg.upper())  #upper()函数，将所有字母都转换成大写 WWW.BAIDU.COM.123
print(msg.lower())  #lower()函数，将所有字母都转换成小写 www.baidu.com.123
print(msg.capitalize())  #capitalize()函数，将首字母都转换成大写，其余小写 Www.baidu.com.123
print(msg.title())  #title()函数，将每个单词的首字母都转换成大写，其余小写 Www.Baidu.Com.123

## Ascll码，用ord()转码，用chr转字符,注意python没有字符概念

msg = 'www.BAIDU.com.123'
for num in msg:
    if 97 <= ord(num) <= 122: #小写字母
        upper_num = ord(num)-32 #大小写字母之前差了32
        #chr()函数可以将编码数值转为字符（python没有字符的概念）
        print (chr(upper_num),end='')
    else:
        print(num,end='')  #不是小写字符，原样输出

        
# int转string
a=100
a_=str(a)
a*=int(a_)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//比较，不要用常量
//char
char s[100];
char v[100];
cin>>s;
cin>>v;
cout<<strcmp(s,v)<<endl;//相同为0，s<v为-1，s>v为1（第一个字符）
//string
string a;
string b="hello";
cin>>a;
if(a==b)...;

//字符串转整形
//char  灵活运用ascii码
char c='6';
int num=c-'0';//char 转 int
num=5;
c=num+'0';//int 转 char
//string 如果是c++11，用stoi
//string->int
string str="123456";
int n=stoi(str);//c++11
int n=atoi(str.c_str());//c++98 devc++
//int->string
n=123456;
str=to_string(n);//c++11 
stringstream ss;//c++98
ss<<n;
str=ss.str();

二进制与位运算

基础运算

  • //：整数除法，返回商的整数部分，忽略余数。
1
print(10 // 3)    # 输出：3
  • %：取模运算符，返回除法的余数。
1
print(10 % 3)    # 输出：1
  • **：幂运算符，计算第一个操作数的第二个操作数次方。
1
print(2 ** 3)    # 输出：8
  • 逻辑运算

逻辑运算符处理布尔值，包括：

  • and：逻辑与，只有两边的操作数都为True时结果才为True。
  • or：逻辑或，只要有一个操作数为True，结果就为True。
  • not：逻辑非，对一个布尔值进行否定。
1
2
3
print(True and False)    # 输出：False
print(True or False)    # 输出：True
print(not True)    # 输出：False
  • 身份运算符，比较两个对象是否为同一对象，而非仅看其值是否相等
    • is：判断两个对象是否引用同一个内存地址，即它们是否是同一个实例。
1
2
3
4
5
6
a = [1, 2, 3]
b = a
print(a is b)    # 输出：True，因为a和b指向同一列表对象

c = [1, 2, 3]
print(a is c)    # 输出：False，尽管a和c的元素相同，但它们是不同的列表实例
  • is not：与is相反，用于检查两个对象是否引用不同的内存地址。
1
2
3
4
5
6
7
8
9
10
a = "hello"
b = "hello"
print(a is not b)    # 输出：False，Python对字符串采用intern机制，所以相同的字符串字面量会指向同一内存地址

class MyClass:
    pass

x = MyClass()
y = MyClass()
print(x is not y)    # 输出：True，因为x和y是MyClass的不同实例

进制转换

x进制转y进制，先将x转为10进制，然后再转为y

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 10进制转x进制
#include<bits/stdc++.h>
using namespace std;
int main(){
	int n,x;
	int p;
	char out[256];
	int cnt=0;
	cin>>n>>x;//输入10 进制n 和要转换的进制x
	//10进制转x进制 
	while(n>0){
		p=n%x;
		if(p<10)out[cnt++]=p+'0';
		else out[cnt++]=(p-10)+'A';//大于10是符号表示 
		n/=x;
	}
	//反序输出
	for(int i=cnt-1;i>=0;i--)
		cout<<out[i]; 
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//x进制转10进制
#include<bits/stdc++.h>
using namespace std;
int main(){
	int ans=0;//记录总数
	int x;
	char inp[256];
	//读取进制数和进制
	scanf("%s%d",&inp,&x);
	int len=strlen(inp);
	for(int i=0;i<len;i++){//注意这里从高位开始 
		ans=ans*x;//每次都要乘一个位全 
		if(inp[i]>='0'&&inp[i]<='9') ans+=(inp[i]-'0');
		else ans+=(inp[i]-'A')+10;
		cout<<ans<<endl;
	}
	printf("%d",ans);
	return 0;
}

位运算

位运算符处理整数的二进制表示，包括：

  • &：按位与，对于两个对应位，如果都是1，则结果为1，否则为0。
  • |：按位或，只要有一个对应位为1，则结果为1，否则为0。
  • ^：按位异或，当两个对应位不同时，结果为1，否则为0。
  • ~：按位取反，对一个数的所有位进行翻转，即将1变为0，0变为1。
  • <<：左移运算符，将数字的所有二进制位向左移动指定的位数。
  • >>：右移运算符，将数字的所有二进制位向右移动指定的位数。

例如：

1
2
print(5 & 3)    # 输出：1，二进制下 5（101）和 3（011）按位与的结果是 1（001）
print(5 | 3)    # 输出：7，二进制下 5（101）和 3（011）按位或的结果是 7（111）

STL C++

stack

1
2
3
4
5
6
7
stark<int> S;//初始化
S.push(1);//入栈
S.push(10);
while(!S.empty()){//判空
    cout<<S.top()<<endl;//栈顶元素
    S.pop();//出栈
}

vector

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
std::vector<int> myVector(5); // 创建一个包含 5 个整数的 vector，每个值都为默认值（0）
std::vector<int> myVector(5, 10); // 创建一个包含 5 个整数的 vector，每个值都为 10
vector<int>demo{ 1,2,3,4,5 };
demo.push_back(7); // 将整数 7 添加到 vector 的末尾
demo.pop_back();
demo.size();
demo.back();//最后一个元素
demo.clear();//释放
auto iter = demo.erase(demo.begin() + 1);//删除元素 2
//删除指定元素
vector<int>demo{ 1,3,3,4,3,5 };
auto iter = std::remove(demo.begin(), demo.end(), 3);//输出{1,4,5}
//二维数组
int a = 2;
int b = 4;
vector<vector<int>> vec(a, vector<int> (b));//2行4列

string

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//构造
string str1;               //生成空字符串
string str2("123456789");  //生成"1234456789"的复制品
string str3("12345", 0, 3);//结果为"123" 从"12345"的第0开始复制3个
string str4("012345", 5);  //结果为"01234" 以"012345"前5个作为粗值
string str5(5, '1');       //结果为"11111" 生成n个字符'1'
string str6(str2, 2);      //结果为"3456789" 将字符串str中从下标stridx开始到字符串结束的位置作为字符串初值
//读取
string s;
cin>>s;
char s[100];
scanf("%s",s);//scanf读char数组
gets(s);//整行读
//插入
string s="Hahah";
str.insert(1,s);//在原串下标为1的字符e前插入字符串s
str1.insert(4,5,s);//在原串下标为4的字符o前插入5个字符s
str2.insert(0,s,1,3);//将字符串s从下标为1的a开始数3个字符，分别是aha，插入原串的下标为0的字符h前

set

1
2
3
4
5
6
7
8
set<int> a;
unordered_set<int> occ;
//长度
int b=0;
a.size();
a.insert(b);
a.erase(b);//移除
a.count(b);//查找返回值为1

memset

1
2
3
4
5
6
7
8
9
功 能: 将s所指向的某一块内存中的每个字节的内容全部设置为ch指定的ASCII值,
块的大小由第三个参数指定,这个函数通常为新申请的内存做初始化工作

用 法: void *memset(void *s, char ch, unsigned n);

对比：
memcpy用来做内存拷贝，你可以拿它拷贝任何数据类型的对象，可以指定拷贝的数据长度；例：char a[100],b[50]; memcpy(b, a, sizeof(b));注意如用sizeof(a)，会造成b的内存地址溢出。

strcpy就只能拷贝字符串了，它遇到'/0'就结束拷贝；例：char a[100],b[50];strcpy(a,b);如用strcpy(b,a)，要注意a中的字符串长度（第一个‘/0’之前）是否超过50位，如超过，则会造成b的内存地址溢出。

map

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
map<string,int> maps;
//插入
maps.insert(pair<int, string>(111, "kk"));
maps[111]="kk";
//maps.find(key) 查找一个元素 返回key的映射的迭代器
map<string,int>::iterator it;
it=maps.find("123");//在容器中寻找值为key为123的元素，返回该元素的迭代器。否则，返回map.end()。

//取值
map->first;//对应key,111
map->second;//对应value,kk

//清空
maps.clear();
//删除一个元素
//迭代器刪除
it = maps.find("123");
maps.erase(it);

//关键字删除
int n = maps.erase("123"); //如果刪除了返回1，否则返回0

//用迭代器范围刪除 : 把整个map清空
maps.erase(maps.begin(), maps.end());
//等同于mapStudent.clear()
maps.begin();//返回指向map头部的迭代器
maps.end();//返回指向map末尾的迭代器
maps.size();
maps.empty();//判空

注意

python

1
2
3
cur=[]
res.append(cur) # 这里是引用，cur变，res变
res.append(cur.copy) # 或者cur[:]y

计时

1
2
3
4
5
6
import time
start = time.perf_counter()


end = time.perf_counter()
print(f"Running time: {end - start} Seconds")
1
2
sort()

1
2
max_value = sys.maxsize
min_value = -sys.maxsize - 1
1
2
3
4
5
double start = clock();
Sleep(1000);
double end = clock();
double last = start - end;
cout << last << "ms" << endl;

c++

  • 超时之memset。N诺很多memset，然而在百度之星一直超时最后发现是memset的问题，当数组很大时比较费时(害我罚了几次时┭┮﹏┭┮)

  • 超时之二维数组开大了，在N诺，

    1
    2
    int store[100005];
    int dp[10005][10005]={0};//前i个，达到重量的可行度

    狠狠超时，然后改成

    1
    2
    int store[1005];
    int dp[1005][1005]={0};//前i个，达到重量的可行度

    (((φ(◎ロ◎;)φ)))

  • oj运行出错：数组开小了

  • oj和答案不对的一个重要原因：没有说明是eof的就得换一种方式读取！！，如果保持eof的方式就会错

    1
    2
    3
    4
    5
    6
    7
    #include <stdio.h>
    int main() {
        int n;
        while (scanf("%d", &n) != EOF) {
            printf("%d\n", (1 + n) * n / 2);
        }
    }

  • 读取方式有可能会造成运行超时：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    //超时版
    int len;
    int v[100001]={0};
    while (scanf("%c", &n) != '\n') {
        if (n != ' ') {
            v[len] = n - '0';
            len++;
        }

        if (n == '\n') break;
    }
    //不超时版
    vector<int> v;
    int i;
    while (cin >> i) {
        v.push_back(i);
        if (cin.get() == '\n') break;
    }

滑动窗口法

438. 找到字符串中所有字母异位词 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        int pLen=p.size();
        int sLen=s.size();
        if(sLen<pLen) return vector<int>();
        //滑动窗口法
        vector<int> ans;
        vector<int> sCount(26);
        vector<int> pCount(26);
        for(int i=0;i<pLen;i++){
            sCount[s[i]-'a']++;//开头的三个先记下
            pCount[p[i]-'a']++;
        }
        if(sCount==pCount) ans.push_back(0);
       for(int i=0;i<sLen-pLen;i++){
            //滑动窗口往右移动一位
            --sCount[s[i]-'a'];
            ++sCount[s[i+pLen]-'a'];
            if(sCount==pCount) ans.push_back(i+1);
       }
       return ans;
    }
};

矩阵

矩阵置零

给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

  • 标记数据，记录二维就用两个
  • 置0直接扫描原矩阵，坐标满足情况就置0，而不是根据目标0去遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m=matrix.size();//行数
        int n=matrix[0].size();//列数
        vector<int> row(m),col(n);
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){//注意这里行列索引要区分
                if(matrix[i][j]==0){//i行j列
                    row[i]=col[j]=1;//标记
                }
            }
        }
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(row[i]||col[j]){
                    matrix[i][j]=0;
                }
            }
        }
    }
};

螺旋矩阵

54. 螺旋矩阵 - 力扣（LeetCode）

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        //对边界进行更新，包括横轴的界和纵轴的界
        vector<int> res;
        if(matrix.empty()) return res;
        int u=0;//上界
        int d=matrix.size()-1;//下界
        int l=0;//左界
        int r=matrix[0].size()-1;//右界
        while(true){
            for(int i=l;i<=r;i++) res.push_back(matrix[u][i]);
            if(++u>d) break;
            for(int i=u;i<=d;i++) res.push_back(matrix[i][r]);
            if(--r<l) break;
            for(int i=r;i>=l;i--) res.push_back(matrix[d][i]);
            if(--d<u) break;
            for(int i=d;i>=u;i--) res.push_back(matrix[i][l]);
            if(++l>r) break;
        }
        return res;
        
    }
};

数据结构及基本操作

数组遍历

1
2
3
def traverse(arr: List[int]):
    for i in range(len(arr)):
        # 迭代访问 arr[i]

链表，迭代递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 基本的单链表节点
class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None

def traverse(head: ListNode) -> None: # -> None 是类型注释的一部分，用于说明函数的返回类型。
    p = head
    while p is not None:
        # 迭代访问 p.val
        p = p.next

def traverse(head: ListNode) -> None:
    # 递归访问 head.val

二叉树 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 基本的二叉树节点
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
        
def traverse(root: TreeNode):
    traverse(root.left) # 递归遍历左子树
    traverse(root.right) # 递归遍历右子树
    
def traverse(root):
    # 前序位置
    traverse(root.left)
    # 中序位置
    traverse(root.right)
    # 后序位置

计算表达式（栈）

后缀表达式的计算(机算)

非常直观，从左往右扫描下一个：

  • 若是操作数，则压入栈
  • 若是运算符号，则弹出两个栈顶元素，执行相应的运算操作，运算结果压回栈顶

image-20240704105049352

中缀表达式

  • 转为后缀
  • 然后运算

分两个栈，一个操作数栈，一个运算符栈

  • 操作数，压入栈
  • 遇到运算符，先判断运算符栈栈顶操作符和当前操作符的级别，如果大于或等于（例如*遇到了+），那就直接用后缀表达式计算方法
    • 即弹出两个操作数，进行运算后，压回操作数栈

括号匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
//括号匹配 栈 ([)]这种可不对 应该先配对好[才能再配对( 
//((([]))) 
int main(){
	string s;
	cin>>s;
	int len=s.length();
	stack<char> st;
	for(int i=0;i<len;i++){
		if(!st.empty()){
			char now=st.top();
			if(s[i]==')'&&now=='('||(s[i]==']'&&now=='[')) st.pop();
			else st.push(s[i]);
		}else{
			//如果为空，入栈
			st.push(s[i]); 
		}
	}
	if(!st.empty()) printf("NO\n");//栈空才成 
	else printf("YES\n");
    return 0;
}

哈夫曼树

1544 - 合并果子 _N诺计算机考研 (noobdream.com)

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。 每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。 因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。 例如有3种果子，数目依次为1，2，9。可以先将1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。

误区：将从小到大排序后依次合并。错误的，例如 5,6,7,8。这里合完5,6为11，再合7,8为15，最后合11和15.因此应当每次挑最小的两个合并，用到优先队列

注意这个运算符的重载为什么符号相反？升序则相反，降序则相同，

在此处定义一个优先队列priority_queue q;

如果要按照以times进行从小到大排列，操作如上。

进行重载<操作符。

意思是如果a.times > b.times成立，那么结构体point a < point b成立。

由于优先队列是按照从大到小排列，所以结构体b会排列到a之前，然而b.times是最小的，所以实现了按照times的从小到大排序,其实用一句话说就是要想b更大那么b.times.C++优先队列(priority queue)及重载运算符_c++ 优先队列重载运算符-CSDN博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;

struct node{
	int x;
	node(int a){x=a;}//构造方法 
};
//重载关系运算符定义优先队列比较关系
bool operator <(const node& a,const node &b){
	return a.x>b.x;
} 
int main(){
	priority_queue<node> q;
	int n,x;
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>x;
		q.push(node(x));
	}
	int anx=0;
	while(q.size()>1){
		//继续合并
		node numa=q.top();//类型是Node 
		q.pop();
		node numb=q.top();
		q.pop();
		anx+=(numa.x+numb.x);
		//插入
		q.push(node{numa.x+numb.x});
	}
	cout<<anx;
	return 0;
}

链表

快慢指针找中点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
"""
链表排序

思想 拆分完后 各自排序，再每部分合并从新排序

快慢指针找中点
"""

# 链表节点
class ListNode:
    def __init__(self,val):
        self.val=val
        self.next=None

def merge(l1,l2):
    if l1 is None:
        return l2
    if l2 is None:
        return l1
    if l1.val<=l2.val:
        # l1放最前 后面继续成链
        l1.next=merge(l1.next,l2)
        return l1
    else:
        l2.next=merge(l1,l2.next)
        return l2
# def merge_sort(node,len):
#     # 找链表中间
#     if node is None or node.next is None or len is 0:
#         return node
# 
#     slow=node
#     mid_loc=len//2
#     print(f"mid_loc:{mid_loc}")
#     for i in range(mid_loc): # 中点
#         slow=slow.next
# 
#     mid=slow.next
#     slow.next=None # 断开
# 
#     # 左右子链归并排序
#     left=merge_sort(node,mid_loc)
#     right=merge_sort(mid,len-mid_loc)
# 
#     return merge_sort(left,right)
def merge_sort(head):
    if head is None or head.next is None:
        return head

    slow = head
    fast = head.next

    # 找到链表的中点
    while fast is not None and fast.next is not None:
        slow = slow.next
        fast = fast.next.next

    mid = slow.next
    slow.next = None

    left = merge_sort(head)
    right = merge_sort(mid)

    return merge(left, right)
def print_list(node):
    while node:
        print(node.val,end=' ')
        node=node.next
if __name__=="__main__":
    # 读取构造链表
    nums=list(map(int,input().split()))
    head=ListNode(int(nums[0])) # 记录头结点
    curr=head # 工作指针
    len=len(nums)
    for num in nums[1:]: # 从1之后开始赋值，第0个已经在头结点了
        curr.next=ListNode(int(num))
        curr=curr.next
    # print_list(head)
    print()
    new=merge_sort(head,len)

    print_list(new)

合并k个有序链表

小根堆，面试常考题，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
"""
合并k个升序列表

思想，因为每个链表都是有序的，因此对他们进行排序，每次取最小的放进去就好了
建立小根堆
"""
import heapq
import random
class Solution(object):
    def mergeKLists(self, lists):
        """
        :type lists: List[ListNode]
        :rtype: ListNode
        """
        if not lists:
            return None
        # 虚拟头结点
        dummy = ListNode(-1)
        p = dummy

        # 优先级队列
        pq = []
        for head in lists:
            if head:
                heapq.heappush(pq, (head.val, head)) # 往pq内建立小根堆

        while pq:
            # 获取最小节点 接到结果链表中

            node = heapq.heappop(pq)[1]  # heapq.heappop()是从堆中弹出并返回最小的值,取1指头节点
            # far=heapq.heappop(pq)[0]
            # print(node.val,far.val)
            p.next = node
            if node.next:
                heapq.heappush(pq, (node.next.val, node.next))
            # p前进
            p = p.next
            # print_priority_queue(pq)
        return dummy.next

单链表的倒数第k个节点

巧妙思想

如何一次遍历链表就到倒数第k个节点呢

用p1先走k，然后设置一个新的p2指向头节点，和p2一起走

当p2走到末尾，p1也就到倒数第k个了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution(object):
    def removeNthFromEnd(self, head, n):
        """
        :type head: ListNode
        :type n: int
        :rtype: ListNode
        """
        # 预防删除头结点的 虚拟节点的重要性
        # 如果是直接从head开始，应对不了规模为1删除为1的，或者是删除的是头结点的情况
        newnode=ListNode(-1)
        newnode.next=head
        p1=newnode
        p2=newnode
        for i in range(n):
            p1=p1.next
        
        # p2开始遍历，直至p1到尾
        # if p1==None:
        #     return None
        while p1.next :
            p1=p1.next
            p2=p2.next
        
        # 删除第n个，即下一个
        p2.next=p2.next.next
        return newnode.next

单链表的中点

快慢指针法

1
2
3
4
5
6
7
8
9
10
def middleNode(head:ListNode):
	# 快慢指针初始化指向head
    slow=head
    fast=head
    # 快指针走向末尾
    while fast and fast.next:# fast判断下一轮直接走出界的情况
        slow=slow.next # 走一步
        fast=fast.next.next # 走两步
    # 慢指针指向中点
    return slow

链表是否有环

力扣第 142 题「环形链表 IIopen in new window」

image-20240313162945782

两个链表是否相交

太巧妙了！
a，b长度可能不同，但是让p1走完a然后走b，p2走完b走a，就能同时达到公共区域
第一次相等的那一刻就是连接点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution(object):
    def getIntersectionNode(self, headA, headB):
        """
        :type head1, head1: ListNode
        :rtype: ListNode
        """
        p1,p2=headA,headB
        while p1!=p2:
            if p1==None:
                p1=headB
            else:
                p1=p1.next
            if p2==None:
                p2=headA
            else:
                p2=p2.next
        return p1

反转链表

理清原地反转的逻辑

  • 先标记出当前节点和下一个
  • 当前节点指向上一个
  • 记录下当前节点
  • 当前节点指针指向下一个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* curr=head;
        ListNode* pre=nullptr;
        while(curr!=nullptr){
            ListNode* next=curr->next;
            curr->next=pre;
            pre=curr;
            curr=next;
        }
        return pre;
    }
};

数组

普通数组

56. 合并区间 - 力扣（LeetCode）

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

排序，时间复杂度简化(思路简化)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        int arr_nums=intervals.size();
        if (arr_nums==0){
            return {};//返回一个空
        }
        sort(intervals.begin(),intervals.end()); //排序一下，根据第一个元素
        vector<vector<int>> res;//最终结果
        for(int i=0;i<arr_nums;i++){
            //如何降低复杂度，就是排序后一个一个存到结果数组
            //显然，结果数组最后一个一定是那个临近的合并元素，如果合不了就直接加入
            int L=intervals[i][0],R=intervals[i][1];
            if(!res.size()||res.back()[1]<L){
                res.push_back({L,R});
                //只有当为空，或者新元素左值大于最后一个右值(无法合并)，才添加
            }else{
                //直接合并取最大
                res.back()[1]=max(res.back()[1],R);
            }
        }
        return res;
    }
};

哈希表

1. 两数之和 - 力扣（LeetCode）

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

从O(N)->O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> hashtable;
        for(int i=0;i<nums.size();i++){
            auto it=hashtable.find(target-nums[i]);
            if(it!=hashtable.end()){
                //找的到满足的
                return {it->second,i};//value对应索引
            }
            hashtable[nums[i]]=i;
        }
        return {};
    }
};

遍历

1
2
3
4
5
6
7
8
9
10
11
map<int,string> myMap={{1,"one"},{2,"two"}};
map<int,string>::iterator iter;
for(iter=myMap.begin();iter!=myMap.end();++iter){
    cout<<iter->first<<":"<<iter->second<<'\n';
}
//或者用while
map<int,string>::iterator iter=myMap.begin();
while(iter!=myMap.end()){
    cout<<iter->first<<":"<<iter->second<<'\n';
    ++i
}

快慢指针技巧

删除重复项
巧妙，利用快慢指针，fast扫到一个新的直接赋值给slow
fast直是在最开始多1，速度是同步的

二分法

167 两数组之和 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def twoSum(self, numbers, target):
        """
        :type numbers: List[int]
        :type target: int
        :rtype: List[int]
        """
        # 非递减排序就可以用类似二分法
        lenth=len(numbers)
        left,right=0,lenth-1
        while left!=right:
            sum=numbers[left]+numbers[right]
            if sum==target:
                return [left+1,right+1]
            if sum<target:
                left+=1
            else:
                right-=1
        return [-1,-1]

5 最长回文子串
核心：对每个字符向两边扩散，注意区分奇偶数情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def longestPalindrome(s: str) -> str:
    res = ""
    for i in range(len(s)):
        # 以 s[i] 为中心的最长回文子串
        s1 = palindrome(s, i, i)
        # 以 s[i] 和 s[i+1] 为中心的最长回文子串
        s2 = palindrome(s, i, i + 1)
        # res = longest(res, s1, s2)
        res = res if len(res) > len(s1) else s1
        res = res if len(res) > len(s2) else s2
    return res

def palindrome(s, l, r):
    while (l >= 0 and r < len(s) and s[l] == s[r]):
        l -= 1
        r += 1
    return s[l+1:r]

调用内置函数

lower_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

例如，求最长上升子序列长度，可以利用升序特点把遍历查找dp改成二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
int LTS_nlgn(){
    int len=1;
    dp[1]=a[1];
    for(int i=2;i<=n;i++){
        if(a[i]>dp[len]){
            dp[++len]=a[i];
        }else{
            int pos=lower_bound(dp,dp+len,a[i])-dp;
            dp[pos]=a[i];
        }
    }
    return len;
}

双指针

15. 三数之和 - 力扣（LeetCode）

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

这题不难，但是很值得思考，各种条件限制，逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int length=nums.size();
        //排序
        sort(nums.begin(),nums.end());
        vector<vector<int>> res;
        for(int first=0;first<length;first++){
            if(first>0&&nums[first]==nums[first-1]){
                continue;
            } // 和上一次不一样 这个很重要也难想，因为first和first-1相同，则二三都可能有两组满足
            int third=length-1;//三指向最后一个来递减
            int target=-nums[first];//达到这个目标
            for(int second=first+1;second<length-1;second++){
                if(second>first+1 && nums[second]==nums[second-1]){
                    continue;
                }
                //为什么是大于，排完序之后，后面是大数
                //third越减，值越小，大于就是为了提前结束后面的没必要再比了，而不至于造成second==thrid跳出后直接second的递增被break了
                while(third>second&&nums[second]+nums[third]>target){
                    third--;
                }
                cout<<second<<','<<third;
                cout<<nums[second-1]<<','<<nums[second];
                if (second==third){
                    //重合
                    break;
                }
                if(nums[second]+nums[third]==target){
                    //满足条件
                    res.push_back({nums[first],nums[second],nums[third]});
                }
            }
        }
        return res;
    }
};

子串

前缀和

560. 和为 K 的子数组 - 力扣（LeetCode）

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。

子数组是数组中元素的连续非空序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count=0;
        int sum=0;
        map<int,int> map;
        map.insert(pair<int,int>(0,1));//初始化前缀和为0
        //遍历
        for(int i=0;i<nums.size();i++){
            sum+=nums[i];
            if(map.find(sum-k)!=map.end()){//找不到返回map.end()
                count+=map[sum-k];//有值对应满足个数 不会计重，因为在此时有多少个满足的就有多少个子数组了，都得算上
            }
            //记得插入
            map[sum]++;
        }
        return count;
    }
};

除自身以外数组的乘积

238. 除自身以外数组的乘积 - 力扣（LeetCode）

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        //这个数等于左边乘积乘右边乘积，只需要多加两个数组把左右都记录就好
        int nsize=nums.size();
        vector<int> LP(nsize),RP(nsize);
        vector<int> ans(nsize);
        LP[0]=1;
        RP[nsize-1]=1;
        for(int i=1;i<nsize;i++){
            LP[i]=LP[i-1]*nums[i-1];
            RP[nsize-i-1]=RP[nsize-i]*nums[nsize-i];
        }
        for(int i=0;i<nsize;i++){
            ans[i]=LP[i]*RP[i];
        }
        return ans;
    }
};

二叉树

动归/DFS/回溯算法都可以看做二叉树问题的扩展，只是它们的关注点不同：

动态规划算法属于分解问题的思路，它的关注点在整棵「子树」。
回溯算法属于遍历的思路，它的关注点在节点间的「树枝」。
DFS 算法属于遍历的思路，它的关注点在单个「节点」。

层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def levelTraverse(root: TreeNode):
    if not root:
        return
    
    q = deque()
    q.append(root)

    # 从上到下遍历二叉树的每一层
    while q:
        sz = len(q)
        # 从左到右遍历每一层的每个节点
        for i in range(sz):
            cur = q.popleft()
            # 将下一层节点放入队列
            if cur.left:
                q.append(cur.left)
            if cur.right:
                q.append(cur.right)

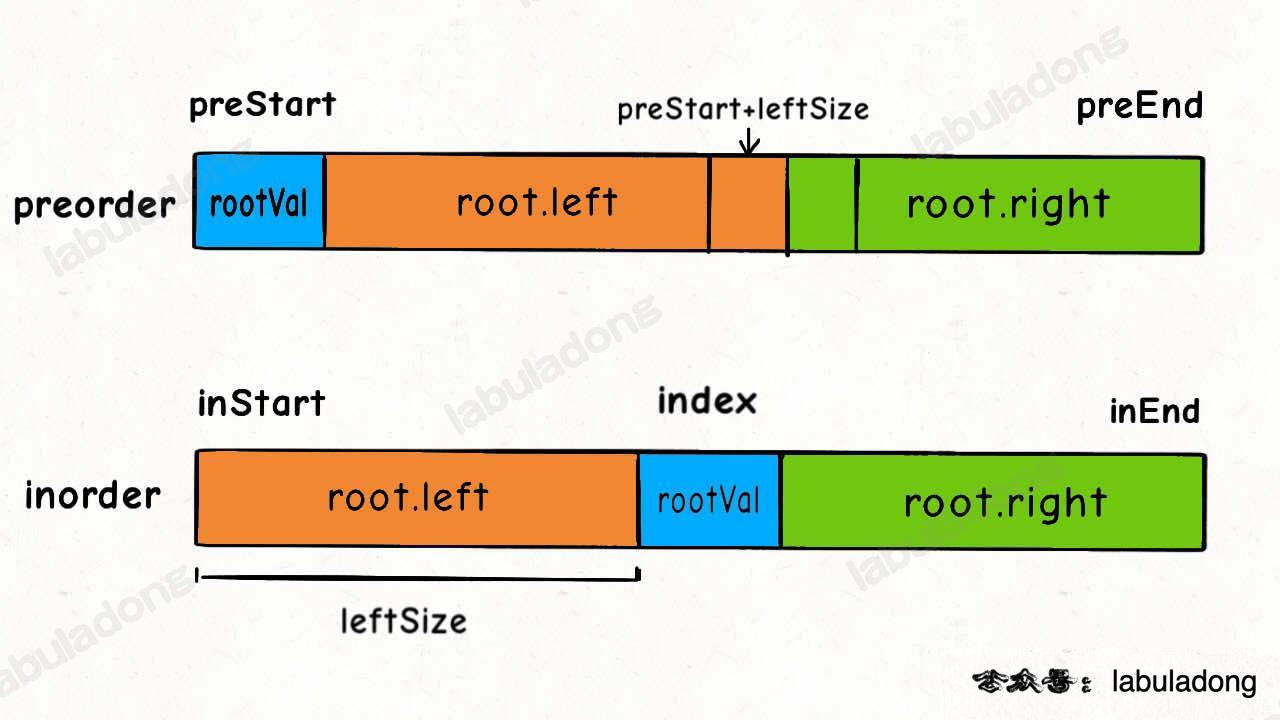
前中序构造

理解前中序数组的结构

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
# 存索引

val2Index={}
class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        for i in range(len(inorder)):#这里和leftSize对应
            val2Index[inorder[i]]=i
        return self.build(preorder,0,len(preorder)-1,inorder,0,len(inorder)-1)
    def build(self,preorder,prestart,preend,inorder,instart,inend):
        if prestart>preend:
            return None
        rootVal=preorder[prestart]
        root=TreeNode(rootVal) # 构造头
        index=val2Index.get(rootVal)
        leftSize=index-instart
        root.left=self.build(preorder,prestart+1,prestart+leftSize,inorder,instart,index-1)
        root.right=self.build(preorder,prestart+leftSize+1,preend,inorder,index+1,inend)

        return root

中序后序

image-20240406013906501

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
var2Index={}
class Solution(object):
    def buildTree(self, inorder, postorder):
        """
        :type inorder: List[int]
        :type postorder: List[int]
        :rtype: TreeNode
        """
        
        for i in range(len(inorder)): #这里和rightSize对应
            var2Index[inorder[i]]=i
        return self.build(postorder,len(postorder)-1,0,inorder,0,len(inorder)-1)
    def build(self,postorder,poststart,postend,inorder,instart,inend):
        if poststart<postend:
            return None
        # if instart > inend:
        #     return None

        rootVal=postorder[poststart]
        root=TreeNode(rootVal)
        index=var2Index.get(rootVal)
        rightSize=inend-index

        root.right=self.build(postorder,poststart-1,poststart-rightSize,inorder,index+1,inend)
        root.left=self.build(postorder,poststart-rightSize-1,postend,inorder,instart,index-1)
        return root

前序后序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
var2Index={}
class Solution(object):
    def constructFromPrePost(self, preorder, postorder):
        """
        :type preorder: List[int]
        :type postorder: List[int]
        :rtype: TreeNode
        """
        for i in range(len(postorder)):
            var2Index[postorder[i]]=i
        return self.build(preorder,0,len(preorder)-1,postorder,len(postorder)-1,0)
    def build(self,preorder,prestart,preend,postorder,poststart,postend):
        if prestart>preend:
            return None
        if prestart==preend:
            return TreeNode(preorder[prestart])
        rootVal=preorder[prestart]
        root=TreeNode(rootVal)
        leftrootVal=preorder[prestart+1]
        #直接折半
        index=var2Index.get(leftrootVal)
        leftSize=index-postend+1
        root.left=self.build(preorder,prestart+1,prestart+leftSize,postorder,index,postend)
        root.right=self.build(preorder,prestart+leftSize+1,preend,postorder,poststart-1,index+1)
        return root

层序遍历bfs

如果利用队列的size进行”分层“

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        
        vector<vector<int>> res;
        if(root==nullptr) return res;
        //队列
        queue<TreeNode*> leaf;
        leaf.push(root);
        TreeNode* p=root;
        while(!leaf.empty()){
           int currentSize=leaf.size();//当前这一层的节点数
           res.push_back(vector<int> ());
           for(int i=1;i<=currentSize;i++){//遍历队列中这一层的节点
                auto node=leaf.front();leaf.pop();
                res.back().push_back(node->val);
                if(node->left) leaf.push(node->left);//新节点加入，不会影响当前层的节点数
                if(node->right) leaf.push(node->right);
           }
        }
        return res;
    }
};

翻转二叉树[递归]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr) return nullptr;
        TreeNode* left=invertTree(root->left);
        TreeNode* right=invertTree(root->right);
        root->left=right;
        root->right=left;
        return root;
    }
};

对称二叉树[题意]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool check(TreeNode *p,TreeNode *q){
        if(!p&&!q) return true;
        if(!p||!q) return false;
        return p->val==q->val &&check(p->left,q->right)&&check(p->right,q->left);
    }
    bool isSymmetric(TreeNode* root) {
        return check(root,root);
    }
};

高精度

十六进制不进位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;
string st="0123456789ABCDEF";//没有就自己写 
int main(){
	string a;
	string b;
	//zz了，从大的开始加啊！高位在低序号 
	while (cin>>a>>b){
		int lena=a.size();
		int lenb=b.size();
		//反序
		reverse(a.begin(),a.end());
		reverse(b.begin(),b.end());
		//思路，每一位当一次加法就好了
		string temp="";//存结果
		for(int i=0;i<max(lena,lenb);i++){
			int temp1=0;
			if(i<lena){
				if(a[i]>'9') temp1+=a[i]-'A'+10;
				else temp1+=a[i]-'0';
			}
			if(i<lenb){
				if(b[i]>'9') temp1+=b[i]-'A'+10;
				else temp1+=b[i]-'0';
			}
			temp+=st[temp1%16];
		}
		reverse(temp.begin(),temp.end());
		cout<<temp<<endl;
		 
	}
	
	return 0;
}

搜索

广度优先BFS

1563 - 迷宫 _N诺计算机考研 (noobdream.com)

队列+访问记录

pop一个，push所有邻接的，并且要标记当前为访问的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<bits/stdc++.h>
using namespace std;
const int maxn=100+5;
char mpt[maxn][maxn];
int vis[maxn][maxn];
//代表上下左右四个动作对应的x，y变化，调用就行 
int dir[4][2]={0,1,1,0,0,-1,-1,0};
struct node{
	int x,y;
	int step;
};
//迷宫 BFS 
int bfs(int sx,int sy){
	//记录访问
	memset(vis,0,sizeof(vis));
	queue<node> q;//使用队列来维护一层层发散的优先级
	q.push(node{sx,sy,0});
	vis[sx][sy]=1;//起点已访问
	int ans=-1;
	while(!q.empty()){
		node now=q.front();
		q.pop();//出队
		if(mpt[now.x][now.y]=='E'){
			//找到终点
			ans=now.step;//记录步数 
			break; 
		} 
		//上下左右四个方向都试一遍 
		for(int i=0;i<4;i++){
			int nx=now.x+dir[i][0];
			int ny=now.y+dir[i][1];
			//判断可走同时未被访问
			if((mpt[nx][ny]=='*'||mpt[nx][ny]=='E')&&vis[nx][ny]==0){
				q.push(node{nx,ny,now.step+1});
				vis[nx][ny]=1;//标记访问 
			} 
		}
	} 
	return ans; 
}
int main(){
	int h,w;
	while(scanf("%d%d",&h,&w)!=EOF){
		if(h==0&&w==0)break;
		int sx=0,sy=0;
		memset(mpt,0,sizeof(mpt));//填充0
		for(int i=1;i<=h;i++){
			scanf("%s",mpt[i]+1);
			for(int j=1;j<=w;j++){
				if(mpt[i][j]=='S'){
					sx=i,sy=j;//记录起点 
				}
			}
		} 
		int ans=bfs(sx,sy);
		printf("%d\n",ans); 
	}
	return 0;
}

递归

Hanoi塔

注意移动要借助才行

1
2
3
hanoi(n-1,p,h,m);//前n-1个 从第一个经过第三个移动到第二个 
hanoi(1,p,m,h);//最后一个经过第二个移动到第三个 
hanoi(n-1,m,p,h);//n-1从第二个经过第一个移动到第三个 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
//汉诺塔 不是简单的一步移动，而是要借助其他的 
int step;//移动步数
 
void hanoi(int n,char p,char m,char h){//表示要将p经过m移动到h 
	if(n==1){
		if((step+1)%5==0){
			//输出格式要求
			cout<<p<<"-->"<<h<<endl; //不能特指，而是通过变量的形式 
		}else cout<<p<<"-->"<<h<<"   ";
		step++;
		return ;
	}
	hanoi(n-1,p,h,m);//前n-1个 从第一个经过第三个移动到第二个 
	hanoi(1,p,m,h);//最后一个经过第二个移动到第三个 
	hanoi(n-1,m,p,h);//n-1从第二个经过第一个移动到第三个 
}
int main(){
	int n;
	while(scanf("%d",&n)){
		if(n==0) break;
		step=0; 
		hanoi(n,'A','B','C');
		cout<<endl;
	} 
	return 0;
}

⭐DFS

实现方式：递归。递归流程->递归树->多叉树

简单来说，BFS和DFS到底有什么区别呢？
对于一棵二义树，
BFS就是二叉树的层次遍历，一层一层的扩展下去。
DS就是二义树的中序遍历，一条路走到底，然后回溯走第二条，直到所有路都走完。

需要注意的是，DFS一般情沉下效率不如BFS,比如求DFS中的迷宫的最短路径使用DFS就会超时。

迷宫

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<bits/stdc++.h>
using namespace std;
char mpt[105][105];
char vis[105][105];
int H=0,W=0;
int dir[4][2]={0,1,0,-1,-1,0,1,0};//上下左右 
int minres=1000000;
//要标记vis！不然就是死循环 
int dfs(int sx,int sy,int res){
	if(res>=minres) return 0;
	if(mpt[sx][sy]=='E'){
		if (res<minres){
			minres=res;
		}
		return res;
	} 
	for(int i=0;i<4;i++){
		int newx=sx+dir[i][0];
		int newy=sy+dir[i][1];
		if((mpt[newx][newy]=='*'||mpt[newx][newy]=='E')&&vis[newx][newy]==0){
			//可以走，递归
			vis[newx][newy]=1;//访问过 
			dfs(newx,newy,res+1);
			vis[newx][newy]=0;//记得回溯，你退出来要留给其他路径走 
		}
	} 
}
int main(){
	
	int sx=0,sy=0;//记录出入口 
	int res=0;
	while(scanf("%d%d",&H,&W)!=EOF){
		if(H==0&&W==0) return 0;
		for(int i=0;i<H;i++){
			for(int j=0;j<W;j++){
				cin>>mpt[i][j];
				if(mpt[i][j]=='S') {
					sx=i;
					sy=j;
				}
			}
		}
		minres=1000000;//注意每轮都要重新设置 
		dfs(sx,sy,0);
		if(minres==1000000) cout<<"-1"<<'\n';
		else cout<<minres<<'\n';
	}
	return 0;
}

图论

存储

邻接矩阵

邻接矩阵是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(邻接矩阵)存储图中的边或弧的信息

arc[i][j]=1,若(vi,vj)∈E或(vj,vi)∈E：0,反之

image.png

特点：

  • 要判断任意两顶点是否有边无边就很容易了；
  • 要知道某个顶点的度，其实就是这个顶点vi 在邻接矩阵中第i 行或（第i 列）的元素之和；
  • 求顶点vi 的所有邻接点就是将矩阵中第i 行元素扫描一遍，arc[i][j]为1 就是邻接点；而有向图讲究入度和出度，顶点vi 的入度为1，正好是第i 列各数之和。顶点vi 的出度为2，即第i 行的各数之和。

邻接表

对于边数相对顶点较少的图，邻接矩阵对空间浪费。邻接表是数组和链表相结合的方法，更加适合，即顶点表(一位数组)和边表(链表)

image.png

从图中可以看出，顶点表的各个结点由data 和firstedge 两个域表示，data 是数据域，存储顶点的信息，firstedge 是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。边表结点由adjvex 和next 两个域组成。adjvex 是邻接点域，存储某顶点的邻接点在顶点表中的下标，next 则存储指向边表中下一个结点的指针。

对于带权的网图，在边表结点定义下加一个weight的数据域，存储权值信息即可

区别

n个顶点e条边的无向图–>邻接表表示有n个顶点表节点，2e个边表结点

n个顶点e条边的有向图–>邻接表表示有n个顶点表节点，e个边表结点

如果图中边的数目远远小于n2称作稀疏图，这时用邻接表表示比用邻接矩阵表示节省空间;

如果图中边的数目接近于n2,对于无向图接近于n*(n-1)称作稠密图,考虑到邻接表中要附加链域，采用邻接矩阵表示法为宜。

并查集(Disjoint Set Union)

Disjoint Set Union：不相交集合并集

解决集合类问题，核心是：树形结构+路径压缩思想，加快区分集合，效率远高于map

并查集还有一个英文名字：union-find sets，从这里可以看出，并查集就是合并(union)查找(find)的集合(set)

代码实现

1.初始化

假设有编号1,2,3,…,n的n个元素，用数组fa[]来存储每个元素的父节点，初始化f[i]=i

2.查询

find，查找i的祖先代表元素

1
2
3
4
int find(int i){
    if(fa[i]==i) return i;//递归出口到达祖先
    else return find(fa[i]);//不断往上查找祖先
}

3.合并

1
2
3
4
5
void unionn(int i,int j){
    int i_fa=find(i);//找到i的祖先 
    int j_fa=find(j);//找到j的祖先
    fa[i_fa]=j_fa;//i的祖先指向j的祖先
}

然而，每次从根开始查都要查n个结点直至到最上面的祖先，大大增加时间开销，因此，出现路径压缩方法，也就是直接指向最大的祖先

graph TD
1-->1
2-->1
3-->2
4-->3

变为

graph TD
1-->1
2-->1
3-->1
4-->1

查询语句变成

1
2
3
4
5
int find(int i){
    if(i==fa[i]) return i;
    else fa[i]=find(fa[i]);//进行路径压缩 更新最
    return fa[i];//返回父节点
}

例题1319 - 畅通工程2 _N诺计算机考研 (noobdream.com)

每个城镇都要可达，最小添加多少。其实可以发现只要是有共同祖先的，都是可以连通的，那么如何判断需要加多少条呢？

  • 判断已经连通的城镇数。在查找合并的时候，如果发现祖先不同，合并的时候联通的城镇数就加1，最后N-sum-1
  • 在判定完后遍历fa，如果等于本身，sum++，最后输出sum-1。这里sum表示有多少个独立的集合，连接这sum个独立集合只需要sum-1条边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
int fa[1001];//记录祖先
int find(int x){
	if(x==fa[x]) return x;//祖先
	fa[x]=find(fa[x]);//压缩 我要祖先的祖先 
	return fa[x];//返回上一级祖先 
} 
int main(){
	int N,M;
	while(cin>>N){
		if(N==0) break;
		cin>>M;
		int sum=0;
		//初始化城市
		for(int i=1;i<=N;i++) fa[i]=i;
		//读取道路
		for(int i=1;i<=M;i++){
			int a,b;
			cin>>a>>b;
			int fxa=find(a);
			int fxb=find(b);
			if(fxa!=fxb){
				//本身不连通，现在联通了
				 fa[fxa]=fxb;
				 sum++;//把对方看作一个单位，那就是多加一个连通的了 
			}
		} 
		printf("%d\n",N-sum-1);
	}
	return 0;
}

很奇怪的是上面代码在N诺如果用scanf反而超时…

最小生成树

最小生成树详解(模板 + 例题)-CSDN博客

一个图中可能存在多条相连的边,我们一定可以从一个图中挑出一些边生成一棵树。这仅仅是生成一棵树,还未满足最小,当图中每条边都存在权重时,这时候我们从图中生成一棵树(n - 1 条边)时,生成这棵树的总代价就是每条边的权重相加之和。

找最小带权图

Kruskal 加边法

Kruskal（克鲁斯卡尔）算法是一种巧妙利用并查集来求最小生成树的算法。

Kruskal算法将一个连通块当做一个集合。Kruskal首先将所有的边按从小到大顺序排序（一般使用快排），并认为每一个点都是孤立的，分属于n个独立的集合。然后按顺序枚举每一条边。如果这条边连接着两个不同的集合，那么就把这条边加入最小生成树，这两个不同的集合就合并成了一个集合；如果这条边连接的两个点属于同一集合，就跳过。直到选取了n-1条边为止。

Prim

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//Kruskal
#include<bits/stdc++.h>
using namespace std;
const int maxn=105;
struct Node{
	int u,v,w;//u,v是两个结点 
}edge[maxn*maxn];//无向图，边重复 
int fa[maxn];
int cmp(Node a,Node b){
	return a.w<b.w;
}
int find(int x){
	if(x==fa[x]) return x;
	fa[x]=find(fa[x]);
	return fa[x];
}
int main(){
	int N,M;
	while(cin>>N){
		if(N==0) break;
		cin>>M;
		//初始化 并查集
		for(int i=1;i<=M;i++) fa[i]=i; 
		for(int i=0;i<N;i++){
			scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].w);
			 
		}
		//根据权值排序
		sort(edge,edge+N,cmp);//确定范围和重载，升序 
		int sum=0;//统计总成本
		int total=0;//统计总边数
		//遍历边表 
		for(int i=0;i<N;i++){
			int fx=find(edge[i].u);
			int fy=find(edge[i].v);
			//最短一条路径，首先他们是否连通
			if(fx!=fy){
				//不连通的
				fa[fx]=fy;
				sum+=edge[i].w;
				total++; 
			} 
		} 
		if(total<M-1){
			//构不成
			cout<<"?"<<"\n"; 
		}else{
			cout<<sum<<"\n";
		}
	}
	
	return 0;
}

最短路径

⭐Floyd

邻接矩阵，最大初始化，三种全遍历循环，k在外头

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;
//邻接矩阵
const int maxn=101;
int mpt[maxn][maxn]; 
int N,M;
void floyd(){
	//k在i,j之间 
	for(int k=1;k<=N;k++){
		for(int i=1;i<=N;i++){
			for(int j=1;j<=N;j++){
				mpt[i][j]=min(mpt[i][k]+mpt[k][j],mpt[i][j]);
			}
		}
	}
}
int main(){

	while(scanf("%d%d",&N,&M)!=EOF){
		if(N+M==0) break;
		//初始化赋最大值
		for(int i=1;i<=N;i++){
			for(int j=1;j<=N;j++){
				if(i==j) mpt[i][j]=0;
				else mpt[i][j]=100000000;
			}
		} 
		for(int i=1;i<=M;i++){
			int vi,vj,w;
			scanf("%d%d%d",&vi,&vj,&w);
			//注意重边！
			if(w<mpt[vi][vj]){
				mpt[vi][vj]=w;
				mpt[vj][vi]=w;//对称 
			} 
			
		}
		floyd();
		printf("%d\n",mpt[1][N]);//起点到终点的最短路径 
	}
	
	return 0;
}

拓扑排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
using namespace std;

const int maxn=505;
bool mpt[maxn][maxn];//记录图 
int lev[maxn];//记录i个结点的入度
vector<int> v[maxn];//表示被i进入的邻居 
//priority_queue<int,vector<int>,greater<int> > q;//最小堆优先队列存放入度为0的优先队列 
priority_queue<int, vector<int>,greater<int> >q;//最小堆优先队列
void topo(int n){
	for(int i=1;i<=n;i++){
		if(!lev[i]) q.push(i);//存放入度为1 
	}
	int flag=0;//统计出队元素个数
	while(!q.empty()){
		int now=q.top();
		q.pop();//踢出 
		if(flag) printf(" %d",now);
		else printf("%d",now);
		flag++;
		for(int i=0;i<v[now].size();i++){//修改邻居的入度 
			int next=v[now][i];
			lev[next]--;
			if(!lev[next]) q.push(next);//入度变0了 
		}
	} 
	if(flag!=n){
		printf("这个图有环，并没有拓扑排序\n");
	}
}

int main(){
	int n,m;
	while(scanf("%d%d",&n,&m)!=EOF){
		memset(lev,0,sizeof(lev));
		for(int i=0;i<=n;i++)v[i].clear();
		while(m--){
			int a,b;
			scanf("%d%d",&a,&b);
			v[a].push_back(b);
			lev[b]++;
		}
	
		topo(n);
		printf("\n");
	}
	return 0;
}

回溯算法

递归和回溯相辅相成

递归函数下面就是回溯内容

回溯搜索：纯暴力搜索算法

  • 组合问题
  • 切割问题
  • 子集问题
  • 排列问题
  • 棋盘问题，n王后，解数独

抽象为n叉数问题，横向节点用for循环表示，纵向深度用递归

1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数){
    if(终止条件){
        在叶子节点搜集结果;
        return;
    }
    for(集合元素){
        处理结点;
        递归;
        回溯;//撤销处理节点结果
    }
    return;
}

回溯三部曲

  • 递归函数参数返回值
  • 确定终止条件
  • 单层递归逻辑(最后一步回溯pop)

组合和排列

回溯用递归模拟了嵌套n层for循环的方式。

回溯：递归嵌套for循环

组合不区分顺序，排列区分

叶子结点收割结果：也就是数组大小等于数的个数

全排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<vector<int>> res;
    int len=0;
    void backtrack(vector<int> now,vector<int>& vis,vector<int>& nums){
        if(now.size()==len){
            res.push_back(now);
        }
        for(int i=0;i<len;i++){
            if(vis[i]==0){//全排列记录
                vis[i]=1;
                now.push_back(nums[i]);
                backtrack(now,vis,nums);
                vis[i]=0;//恢复标记
                now.pop_back();//恢复状态
            }
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        len=nums.size();
        vector<int> vis(len);
        backtrack(vector<int>(),vis,nums);
        return res;
    }
};

排序算法

堆排序

堆是一个完全二叉树，只有最后一层不满，且只能没有右子节点

堆序性：

  • 大根堆
  • 小根堆

存储：

用一位数组，从上到下从左到右给每个节点编号，这个就是在数组的存储序号

这样存储有一个规律，设节点下标为i：

  • 左子节点下标为2i+1
  • 右子节点下标为2i+2

上滤和下滤：O(logN)

  • 当根节点不满足堆序性，子树都满足时(以大根堆为例)，把该节点和最有子树最大值比较然后换位，直到没有小于或者到达最后一层，这就是下滤
  • 同理，上滤就是和根比较，小于就换，直到遇到比他小的或到根节点

建堆：

  • 自顶向下建堆法 O(NlogN)
    • 将新元素放到堆的最后一位，然后进行上滤操作
  • 自下而上建堆法 O(n)
    • 首先将下面的调整成堆，然后对父节点进行下滤，直到根节点操作完毕

应用：

  • 优先队列(小根堆)，是插入队列后弹出最小元素。直接弹出排好序的堆的根节点
    • 弹出后，将最后一个元素放到根节点，重新进行下滤就有序了
  • 插入操作，插入到尾部，然后进行上滤

堆排序：

就是将优先队列的所有元素依次弹出即可！

image-20240511152631639

image-20240511152655004

然而实际为了考虑空间复杂度会利用原来堆的空余位置建立有序区

如何做：

  1. 先调整为最大堆(最大元素在顶上)
  2. 将根节点和最后一个元素(不一定最小)交换，此时最后一个位置就是有序区的开始
  3. 然后将新的根节点进行下滤，完成后根节点又是最大的，把它的倒数第二个交换(倒数第一个位置已经是有序区了)，这时有序区延伸到倒数第二个位置
  4. 重复扩大有序区，直到全部有序，这是会发现，大的在最后，小的在最前，也就是递增序列

因此：形成递增则构造最大堆，递减则构造最小堆

【从堆的定义到优先队列、堆排序】 10分钟看懂必考的数据结构——堆_哔哩哔哩_bilibili

动态规划

核心是：最优子结构。不都是(如乘积最大子数组，根据题意适当变动

  • 动规基础
  • 背包问题
  • 打家劫舍
  • 股票问题
  • 子序列问题

重要点：

  • dp数组以及下界的含义，dp[i][j]、dp[i]
  • 递推公式
  • dp数组如何初始化,0?1?…
  • 遍历顺序
  • 打印dp数组，看看输出结果是否正确

斐波那契，dp数组降到1维，动态变化三个值即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
    def fib(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n==0:
            return 0
        if n==1:
            return 1
        dp_i=1
        dp_ii=1
        dp_iii=1
        for i in range(2,n):
            dp_iii=dp_i+dp_ii
            dp_i=dp_ii
            dp_ii=dp_iii
        return dp_iii

跳楼梯

照动态规划思想，我们可以先分析下问题，每次都有两种跳法，分别是一阶或者两阶，那么如果当前是第n 个台阶，那么跳法是不是是(n-1)台阶的跳法数加上(n-2)台阶的跳法数？如果划算成公式是F(n) = F(n-1)+F(n-2)。

这里容易有误区，为什么不是F(n-1)加一步，然后F(n-1)加两步(跳一个和两个)。首先F(n-1)到F(n)此时只有唯一的一种操作，那么到F(n)的步数就是F(n-1)。而F(n-1)跳一步的情况已经被F(n-1)包括了，此时只有跳两步的操作，同上，只有F(n-2)的情况。因此F(n)=F(n-1)+F(n-2)

如果测试样例一直过不了，考虑数据类型，要开long long

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std;
int main(){
	int n;
	while(scanf("%d",&n)!=EOF){
		long long tff=1,tf=2,fin=2;//开long long才够
		if(n<=2) {
			cout<<n;
		}
		else{
			for(int i=3;i<=n;i++){
				fin=tff+tf;
				tff=tf;
				tf=fin;	
			}
			cout<<fin;
		}
	}
	return 0;
}

最大子段和

最大序列和

可能自己就已经大于加上前面的了(前面时负数)!!!!

并且，子序列是连续的！

对于dp输出，dp[i]表示到第i的最大序列和，可能是前一个加上自己或者仅是自己。

然而，最长的不一定是最大的，如果前面已经达到最大的了呢？那么我们需要维护一个最大值，如果大于他，更新。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<bits/stdc++.h>
using namespace std;
long long ans[1000001];
int main(){
	int N;
	while(scanf("%d",&N)!=EOF){
		//维护一个最大值
		long long maxn=-100000000; 
		long long fin=-100000000;
		for(int i=0;i<N;i++){
			cin>>ans[i];
			maxn=max(maxn+ans[i],ans[i]);
			if(maxn>fin) fin=maxn;
		} 
		//每个都要找子序列，然后跟新最大的
		 
		cout<<fin<<"\n";
		
	}
	return 0;
}

字符串区间翻转 题意转换

1642 - 字符串区间翻转 _N诺计算机考研 (noobdream.com)

我们把01字符串的0变成1,1变成-1，然后构成一个1和-1的字符串。
对这样一个字符串去求它的最大子段和即可，最后再把1的个数加上就是最终的答案。

为什么可以这样?

  • 本质是求0和1最大数量差的区间
  • 最大序列和就意味着反转后，这里会在01反转互相抵消之下又多出多少个1，因此和原本的1加上，就是翻转后1的个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;
int dp[10000005];
char s[10000005];
int a[10000005];
int _max(int x,int y){
	return x>y?x:y;
}
int main(){
	int n;
	while(scanf("%d",&n)!=EOF){
		scanf("%s",s);//读取字符串
//		cout<<s;
	
		//遍历构建构建新数组，0->1,1->-1 
		for(int i=0;i<n;i++){
			if(s[i]=='0') a[i]=1;
			else a[i]=-1;
//			cout<<a[i]<<" ";
		}
		int maxn=0;
		dp[0]=a[0];
		
		for(int i=1;i<n;i++){
			dp[i]=_max(dp[i-1]+a[i],a[i]);//最大序列和
			if(dp[i]>maxn) maxn=dp[i]; 
//			cout<<dp[i]<<"\n";
		}
		for(int i=0;i<n;i++)
			if(s[i]=='1') maxn++;
		cout<<maxn<<"\n"; 
	}
	return 0;
}

最长递增子序列

既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到这些子序列末尾，就可以形成一个新的递增子序列，而且这个新的子序列长度加一。

1
2
3
4
5
for (int j = 0; j < i; j++) {
    if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1);
    }
}

利用函数lower_bound

1
2
3
4
5
6
7
8
9
10
11
12
13
int LTS_nlgn(){
    int len=1;
    dp[1]=a[1];
    for(int i=2;i<=n;i++){
        if(a[i]>dp[len]){
            dp[++len]=a[i];
        }else{
            int pos=lower_bound(dp,dp+len,a[i])-dp;//从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
            dp[pos]=a[i];
        }
    }
    return len;
}

求和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
using namespace std;
int a[1002];
int dp[1002];
int main(){
	int N;
	while(scanf("%d",&N)!=EOF){
		for(int i=1;i<=N;i++) cin>>a[i];
		int maxn=0;
		for(int i=1;i<=N;i++){
			dp[i]=1;//清空上一个样例
			for(int j=1;j<=i;j++){
				if(a[j]<a[i]){
					//满足升序
					dp[i]=max(dp[i],dp[j]+a[i]);
					if(dp[i]>maxn) maxn=dp[i];
				} 
			} 
		}
		cout<<maxn<<"\n";
	}
	
	return 0;
}

最长公共子序列 二维dp

dp[i, j]代表a 字符串前i 个字符组成的子串和b 字符串前j 个字符组成的子串的LCS。
那么
dp[i, j] = 0 if i = 0 or j = 0
dp[i, j] = dp[i - 1, j - 1] + 1 if i, j > 0 and ai = bj
dp[i, j] = max{dp[i, j - 1], dp[i - 1, j]} if i, j > 0 and ai != bj 至少一个满足

注意，这里0留空了，dp数组从1开始，因此对比是要比较s1[i-1]和s2[j-1]，最后输出是输出dp[strlen(s1)][strlen(s2)]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<bits/stdc++.h>
using namespace std;
char s1[101];
char s2[101];
int dp[101][101];
int main(){
	while(scanf("%s",s1)!=EOF){
		scanf("%s",s2);
		for(int i=1;i<=strlen(s1);i++){
			for(int j=1;j<=strlen(s2);j++){
				if(s1[i-1]==s2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
				else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
//				maxn=max(maxn,dp[i][j]);
			}
		}
		cout<<dp[strlen(s1)][strlen(s2)];
	}
	return 0;
}

最少编辑长度

字符串动规，递归超时

72. 编辑距离 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution(object):
    def minDistance(self, word1, word2):
        """
        :type word1: str
        :type word2: str
        :rtype: int
        """
        m,n=len(word1),len(word2)
        dp=[[0]*(n+1) for _ in range(m+1)]
        for i in range(1,m+1):
            dp[i][0]=i
        for j in range(1,n+1):
            dp[0][j]=j
        for i in range(1,m+1):
            for j in range(1,n+1):
                if word1[i-1]==word2[j-1]:
                    dp[i][j]=dp[i-1][j-1]
                else:
                    dp[i][j]=min(
                        dp[i-1][j]+1,
                        dp[i][j-1]+1,
                        dp[i-1][j-1]+1
                    )
        return dp[m][n]

乘积最大子数组

152. 乘积最大子数组 - 力扣（LeetCode）

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续

子数组

（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

关键：当前位置的最优解未必是由前一个位置的最优解转移得到的->根据正负性进行分类讨论

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
    def maxProduct(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        length=len(nums)
        dpmax=[0]*length
        dpmin=[0]*length
        dpmax[0]=nums[0]
        dpmin[0]=nums[0]
        for i in range(1,length):
            dpmax[i]=max(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])
            # 「负得更多」，即尽可能小
            dpmin[i]=min(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])
            
        print(dpmax)
        return max(dpmax)

完全平方

279. 完全平方数 - 力扣（LeetCode）

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

数学拆分为jxj+i-jxj，i-jxj就是一个子问题，遍历枚举

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
    def numSquares(self, n):
        """
        :type n: int
        :rtype: int
        """
        dp=[0]*(n+1)
        dp[0]=0
        for i in range(1,n+1):
            j=1
            minn=sys.maxsize 
            while j*j<=i:
                minn=min(dp[i-j*j],minn)
                j+=1
            dp[i]=minn+1 # 超分成i-j*j的子集+j的情况，这个1就是代表j
        # print(dp)
        return dp[n]

背包问题

第一步要明确两点，「状态」和「选择」。只要给几个物品和一个背包的容量限制，就形成了一个背包问题呀。所以状态有两个，就是「背包的容量」和「可选择的物品」。

对于每件物品，你能选择什么？选择就是「装进背包」或者「不装进背包」嘛。

第二步要明确 dp 数组的定义。

两个状态->一个二维dp数组

dp[i][w] 的定义如下：对于前 i 个物品，当前背包的容量为 w，这种情况下可以装的最大价值是 dp[i][w]。 (前i个任取，放到w容量的背包)

比如说，如果 dp[3][5] = 6，其含义为：对于给定的一系列物品中，若只对前 3 个物品进行选择，当背包容量为 5 时，最多可以装下的价值为 6。

根据这个定义，我们想求的最终答案就是 dp[N][W]。base case 就是 dp[0][..] = dp[..][0] = 0，因为没有物品或者背包没有空间的时候，能装的最大价值就是 0。

第三步，根据「选择」，思考状态转移的逻辑。

如果你没有把这第 i 个物品装入背包，那么很显然，最大价值 dp[i][w] 应该等于 dp[i-1][w]，继承之前的结果。

如果你把这第 i 个物品装入了背包，那么 dp[i][w] 应该等于 val[i-1] + dp[i-1][w - wt[i-1]]。(定义i从1开始，所以 val[i-1] 和 wt[i-1] 表示第 i 个物品的价值和重量)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

def knapsack(W: int, N: int, wt: List[int], val: List[int]) -> int:
    assert N == len(wt)
    # 初始化一个二维数组，用于存储状态
    # dp[i][j] 表示将前 i 个物品装入容量为 j 的背包中所获得的最大价值
    dp = [[0] * (W + 1) for _ in range(N + 1)]
    # 开始进行递推
    for i in range(1, N + 1):
        for w in range(1, W + 1):
            if w - wt[i - 1] < 0:
                # 当前商品 i 的重量已经超过了 w，无法被放入当前容量为 w 的背包中，只能选择不装入背包
                dp[i][w] = dp[i - 1][w]
            else:
                # 当前商品 i 的重量小于等于当前容量 w，可以尝试将其放入背包中
                # 取最大值，考虑是将其放入之前的最优方案中还是选择不放
                dp[i][w] = max(
                    dp[i - 1][w - wt[i - 1]] + val[i - 1],# 放第i个物品，那么就要从i-1个物品中加上第i个，注意重要要从当前的减去第i个物品的开始加.同时，因为val从0开始放，所以第i个重量是val[i-1]
                    dp[i - 1][w] # 啥都不放
                )
    # 返回最大价值
    return dp[N][W]

简化版背包

值得思考的简化版背包

设有一个背包可以放入的物品重量为S，现有n件物品，重量分别是w1，w2，w3，…wn。

问能否从这n件物品中选择若干件放入背包中，使得放入的重量之和正好为S。

如果有满足条件的选择，则此背包有解，否则此背包问题无解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
//int dp[1001][1001];//代表前i 个物品背包容量最大为j 最多能装的物品总重量
int dp[1005][1005]={0}; 
int ths[1005];
int main(){
	int s,n;
	while(scanf("%d%d",&s,&n)!=EOF){
		for(int i=0;i<n;i++){
			scanf("%d",&ths[i]);
		}
		memset(dp, 0, sizeof(dp));//必要清空 
		dp[0][0]=1;//前i件物品凑成重量0可行性为1  这一步初始化关键！
		for(int i=1;i<=n;i++){
			for(int j=s;j>=0;j--){
				if(dp[i-1][j]==1) dp[i][j]=1;//前i-1已经可以满足
				if(j>=ths[i-1]&&dp[i-1][j-ths[i-1]]==1) dp[i][j]=1;//能够凑成 
				
			}
		}
		if(dp[n][s]==1) printf("YES\n");
		else printf("NO\n");
	}
	
	return 0;
}

常规01背包

1567 - Buyer _N诺计算机考研 (noobdream.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
int cost[1005];
int pop[1005];
int dp[1005][1005];//表示前i个到达费用j的受欢迎指数 
int main(){
	int M,N; //M钱数,N种类 
	vector<int> buy[105];//记录方案 
	while(scanf("%d%d",&M,&N)!=EOF){
		for(int i=1;i<=N;i++) cin>>cost[i]>>pop[i];
		for(int i=1;i<=N;i++){
			for(int j=0;j<=M;j++){ //从0块开始 
				//放与不放 
				//如果大于当前的
				if(j>=cost[i]) {
					if(dp[i-1][j-cost[i]]+pop[i]>dp[i-1][j]){
						buy[j]=buy[j-cost[i]];
						buy[j].push_back(i);//追加
						dp[i][j]= dp[i-1][j-cost[i]]+pop[i];
					}else dp[i][j]=dp[i-1][j];
				}
				
				else //不够买当前的 
					dp[i][j]=dp[i-1][j];
			}
		}
		//输出受欢迎
		printf("%d\n",dp[N][M]);
		if(dp[N][M]!=0){
			for(int i=0;i<buy[M].size();++i) printf("%d ",buy[M][i]);
			printf("\n");
		} 
	}
	
	return 0;
}

状态压缩

数论

质数

判断素数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;

int main(){
	int n;
	scanf("%d",&n);
	//注意1的情况
	if(n==1) {
		printf("2"); 
		return 0;
	}
	for(int i=n;;i++){//它本身如果是，直接输出，否则它+1开始找！
		//输出大于整数的素数
		 int flag=0;
		 for(int j=2;j<sqrt(n);j++){//判断素数 
		 	if(i%j==0){
		 		flag=1;
		 		break;
			 } 
		 }
		 if(flag==0){//是素数，输出 
		 	printf("%d",i);
		 	break;
		 }
		 //不是的话就从+1开始找 
	}
	
	return 0;
}

分解质因素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
//质因素个数 
int main(){
	int N;
	int nums[1001];
	while(scanf("%d",&N)!=EOF){
		int cnt=0;
		int i=2;
		while (i*i<=N){
			if(N%i==0){
				nums[cnt++]=i;
				N/=i;
			}else{
				i+=1;
			}
		}
		//最后跳出循环的N结果如果大于1就是一个素数 
		if(N>1){
			nums[cnt++]=N;
		}
		printf("%d\n",cnt);
		for(int i=0;i<cnt;i++)
			printf("%d ",nums[i]);
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 分解质因素
def prime_factor(num):
    factors = []
    i = 2
    while i * i <= num:
        if num % i == 0:
            factors.append(i)
            num = num // i
        else:
            i += 1
    if num > 1:
        factors.append(num)
    return factors

# 或者 用于统计质因数指数
n=int(input())
i=2
while i*i<=n:
    while not n%i:
        n//=i
        print(i,end=' ')

if n!=1:
    print(n)

为什么i一般到根号x就足够了呢，我们想想，如果两个数相乘等于x，那么这两个数只有两种情况，要么都等于根号x，要么一个大于根号x，一个小于根号x

素数筛选

我们要知道一个合数，一定是某个质因素的倍数

埃式筛法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int main(){
	int N=1e6,cnt=0;
	//埃式筛，一个合数一定是某个质因素的倍数，因此
	//找出一个质数，把他所有倍数筛掉(不包括自己
	for(int i=2;i<=N/i;i++){//这里到N/i即可 
		if(!pri[i])//如果没被筛掉，说明是质数。如7，它不可能被前面的筛掉 
			for(int j=2*i;j<=N;j+=i){
			//从2倍开始，不包括自己 
				pri[j]=i;
			}
	} 
	//统计个数
	for(int i=2;i<=N;i++) if(!pri[i])cnt++;
	printf("%d",cnt); 
	return 0;
}

欧拉筛法、

埃式筛法有个问题，公倍数会被重复筛好几次，比如12，会被2筛也会被3筛

加一个数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int main(){
	int N=1e6,cnt=0;
	int pp=0;
	for(int i=2;i<=N;i++){ //注意这里范围，s
		//如果没被筛，说明是素数，存到prime数组
		if(!pri[i]) prime[++pp]=i;
		//接下来遍历prime来筛 
		for(int j=1;prime[j]*i<=N;j++){//目前所有素数的i倍
			pri[prime[j]*i]=1;//筛素数倍数 
			if(i%primes[j]==0) break;//这一步关键 防止重复筛
			//比如，4，假设当j到3， prime[j]*i=12，这是会筛掉12
			//但是有了这一步，当j是2的时候已经break了，这就保证了
			//12不会被重复筛，而是留到当 prime[j]为6时被掉了 
		} 
	}
    //最后直接用primes这个素数数组即可
	return 0;
}

应该时没比埃式筛快多少的

例题

给定n，a求最大的k，使n！可以被a^k整除但不能被a^(k+1)整除。1284 - 整除问题 _N诺计算机考研 (noobdream.com)

转换思维

背住最大公约数，最小公倍数，Floyd 算法！！！

最小公倍数* 最大公约数 = 两数乘积 ，即 x*y=LCM(x, y)*GCD(x, y)。而最大公约数可以使用[辗转相除法](https://zhuanlan.zhihu.com/p/31824895#:~:text=辗转相除法， 又名欧几里得算法（Euclidean algorithm），目的是求出两个正整数的最大公约数。,它是已知最古老的算法， 其可追溯至公元前300年前。 这条算法基于一个定理： 两个正整数a和b（a>b），它们的最大公约数等于a除以b的余数c和b之间的最大公约数。)求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
# 最大公倍数、最小公约数
#最大公约数和最小公倍数
a = int(input('请输入第一个数: '))
b = int(input('请输入第二个数: '))
Min = min(a,b)
Gys = 1
for i in range(1,int(Min+1)):
    if a%i == 0 and b%i == 0:
        Gys = i
print('最大公约数为：%d' %Gys)
Gbs = a*b / Gys
print('最小公倍数为:%d' %Gbs)

辗转相除法基于原理“两个整数的最大公约数等于其中较小值与两数相除余数的最大公约数

GCD(a,b)=GCD(b,a%b)

1
2
3
4
5
6
7
8
9
10
11
a = int(input('请输入第一个数: '))
b = int(input('请输入第二个数: '))
m,n=a,b
if a<b:
    m,n=b,a
r=m%n
while n!=0:
    m=n
    n=r
    r=m%n
print(n)
1
2
3
4
5
//如果结果为1，说明二者是最简真分数
int gcd(int a,int b){
	if(b==0) return a;//结束
	else return gcd(b,a%b);//辗转相除 
}

Floyd算法

原理很简单：
一个点 i 到另一个点 j 的最短路径无非有两种：

  1. 直接到达( i –> j )
  2. 通过走其他点(k1, k2 … kn)，一个或多个点到达（ i –> k1–>k2–> … –> j )
1
2
3
4
5
for k in range(n):
	for i in range(n):
		for j in range(n):
			graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])

完全平方数

一个整数 a 是一个完全平方数，是指它是某一个整数的平方，即存在一个整数 b，使得 a = b ^ 2。给定一个正整数 n，请找到最小的正整数 x，使得它们的乘积是一个完全平方数。

给定一个正整数 n，请找到最小的正整数 x，使得它们的乘积是一个完全平方数。

一个完全平方数，他的质因数的指数都是偶数

所以要凑的话，就得分解质因数，不是偶数的补上，一直乘

留意未分尽的情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
n = int(input())
i = 2
cnt = 0
res = 1
while i * i <= n:
    cnt = 0
    while not n % i:
        n //= i
        cnt += 1
    if cnt % 2:
        res *= i
    i+=1

if n != 1:
    res *= n

print(res)

高精度

string[0]输出反而代表数字的高位，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;

string couculate(string a,string b){
	int carry=0;//计算进位
	if(a.length()<b.length()) a.swap(b);
	string res(a.length(),0);//设置
	b.insert(0,a.length()-b.length(),'0');//较短的字符补0 
	for(int i=a.length()-1;i>=0;i--){
		int sum=(a[i]-48)+(b[i]-48)+carry;
		carry=sum/10;
		res[i]=sum%10+48;
	}
	if(carry!=0){
		res.insert(res.begin(),carry+48);
	}
	return res;
	
}

int main(){
	string a,b;
	while(cin>>a>>b){
		cout<<couculate(a,b)<<endl;
	}
	
	return 0;
}

SCNUOJ练习题

P01 最大二叉树

  • 读取，构造二叉树
  • 构造最大二叉树
    • 特殊情况–只有一个元素
    • 找最大值
    • 判左右是否空，左右递归
    • 返回根节点
  • 前序遍历函数
    • 终止情况：为空结点，返回
    • 排除叶子结点情况
    • 其他：输出结点，递归左右
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
// 最大二叉树
#define _CRT_SECURE_NO_WARNINGS
# include<iostream>
# include<vector>
using namespace std;
//定义二叉树
struct TreeNode
{
    int val;
    TreeNode* left;
    TreeNode* right;
    //无参
    TreeNode() :val(0), left(nullptr), right(nullptr) {}
    //有参
    TreeNode(int x) :val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) :val(x), left(left), right(right) {}
};
//前序遍历
void PreOrder(TreeNode* tr) {
    if (tr == NULL) {
        cout << "null" << " ";
        return;
    }
    //叶子节点的两个子空节点要去掉不输出！否则会多输出一对null
    else if (tr->left == NULL && tr->right == NULL) {
        cout << tr->val<<" ";
        return;
    }
    else {
        cout << tr->val << " ";
        PreOrder(tr->left); //递归左子树
        PreOrder(tr->right); //递归右子树
    }
}
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        TreeNode* node = new TreeNode(0);
        if (nums.size() == 1) {
            //只有一个元素，直接返回
            node->val = nums[0];
            return node;
        }
        //中间找最大
        int maxValue = 0;
        int maxValueIndex = 0;//找最大值
        for (int i = 0; i < nums.size(); i++)
        {
            if (nums[i] > maxValue) {
                maxValue = nums[i];
                maxValueIndex = i;
            }
        }
        node->val = maxValue;
        //左边还有元素
        if (maxValueIndex > 0)
        {
            //newVec左闭右开
            vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
            //左子树的构造就是对左边递归
            node->left = constructMaximumBinaryTree(newVec);
        }
        if (maxValueIndex < (nums.size() - 1)) {
            //右边递归
            vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
            node->right = constructMaximumBinaryTree(newVec);
            
        }
        return node;

    }
};

int main() {
    int a ;
    vector<int> nums;
    //读取
    while (scanf("%d", &a) != EOF) {
        nums.push_back(a);
    }
    Solution s1;
    TreeNode *re;
    re=s1.constructMaximumBinaryTree(nums);
    PreOrder(re);
    return 0;
}

！P02. [算法课分治] 寻找多数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//寻找多数
#include<iostream>
using namespace std;
//返回特定元素在特定数组中出现的次数
int traverse(int nums[], int pivot, int left, int right) {
	int num = 0;
	for (int i = left; i <= right; i++) {
		if (nums[i] == pivot) num++;
	}
	return num;
}
int findM(int nums[], int left, int right) {
	//规模为1直接求解
	if (left == right) return nums[left];
	//分解
	int mid = (left + right) / 2;
	int leftNum = findM(nums, left, mid);
	int rightNum = findM(nums, mid+1, right);
	//当前数组的解为两个数组解在当前数组出现次数较大的解
	if (leftNum == rightNum) return leftNum;
	else {
		int lcount = traverse(nums, leftNum, left, right);
		int rcount = traverse(nums, rightNum, left, right);
		return lcount > rcount ? leftNum : rightNum;
	}
}

int main() {
	//读取
	int n;
	int nums[10001] = { 0 };
	cin >> n;
	int a;
	for (int i = 0; i < n; i++) {
		cin >> a;
		nums[i] = a;
	}
	cout << findM(nums, 0, n - 1);
	return 0;
}

P03. [算法课分治] 找到最大子序和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<iostream>
#include<vector>
#include <climits>
using namespace std;

int getMaxNum(int a, int b, int c) {
    if (a > b && a > c) {
        return a;
    }
    if (b > a && b > c) {
        return b;
    }
    return c;
}
int maxSumRec(int data[], int left, int right) {
    if (right - left == 1) {
        //如果当前序列只有一个元素
        return data[left];
    }
    int center = (left + right) / 2;//计算当前序列的分裂点
    int maxLeftSum = maxSumRec(data, left, center);
    int maxRightSum = maxSumRec(data, center, right);
    //计算左边界最大子序列和
    int leftBonderSum = 0;
    int maxLeftBonderSum = data[center - 1];
    for (int i = center - 1; i >= left; i--) {
        leftBonderSum += data[i];
        if (maxLeftBonderSum < leftBonderSum) {
            maxLeftBonderSum = leftBonderSum;
        }
    }
    //计算右边界最大子序列和
    int rightBonderSum = 0;
    int maxRightBonderSum = data[center];
    for (int i = center; i < right; i++) {
        rightBonderSum += data[i];
        if (maxRightBonderSum < rightBonderSum) {
            maxRightBonderSum = rightBonderSum;
        }
    }
    //返回当前序列最大子序列和
    return getMaxNum(maxLeftBonderSum + maxRightBonderSum, maxLeftSum, maxRightSum);
}
int main() {
	int n;
	int v1[1000000];
	cin >> n;
	int t;
	for(int i=0;i<n;i++)
	{
		cin >> t;
		v1[i]=t;//读入
	}
	
    cout<<maxSumRec(v1, 0, n);
}

P04. [算法课分治] 找到 k 个最小数

就是一个快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>
using namespace std;

int part(int* a, int low, int height) {
	int i = low, j = height, pviot = a[low]; //这里是low就要从j开始，要从i开始就得是height
	while (i < j) {
		
		while (a[j]>pviot&&i<j)
		{
			j--;
		}
		if (i < j) {
			swap(a[i++], a[j]);//交换后i后移
		}
		while (a[i] < pviot && i < j)
		{
			i++;
		}
		if (i < j) {
			swap(a[i], a[j--]);//交换后，j前移
		}
	}
	return i;//返回最终划分完成后基准元素所在的位置
}
void Quicksort(int* a, int low, int height) {
	int mid;
	if (low < height) {
		mid = part(a, low, height);
		//分治
		Quicksort(a, low, mid - 1);
		Quicksort(a, mid + 1, height);
	}
}
int main() {
	int n,a,k;
	int nums[10001] = { 0 };
	cin >> n >> k;
	for (int i = 0; i < n; i++) {
		cin >> a;
		nums[i] = a;
	}
	Quicksort(nums, 0, n - 1);
	for (int i = 0; i < k; i++) {
		cout << nums[i] << " ";
	}
	return 0;
}

P05. [算法课分治] 寻找第 k 个最大元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<iostream>

using namespace std;

int part(int* a, int low, int height) {
	int i = low, j = height, pviot = a[low];
	while (i < j) {
		while (a[j] > pviot && j > i) {
			j--;
		}
		if (i < j) {
			swap(a[i++], a[j]);//交换后，i后移
		}
		while (a[i] < pviot && i < j) {
			i++;
		}
		if (i < j) {
			swap(a[i], a[j--]);
		}
		
	}
	return i;//返回最终划分完成后基准元素所在的位置
}

void Quicksort(int *a, int low,int height) {
	int mid;
	if (low < height) {
		mid = part(a, low, height);
		Quicksort(a, low, mid - 1);
		Quicksort(a, mid + 1, height);
	}
}
int main() {
	//数据读取
	int len, k;
	int a[1000];
	int t;
	cin >> len >> k;
	for (int i = 0; i < len; i++) {
		cin >> t;
		a[i] = t;
	}
	//快速排序
	Quicksort(a, 0,len-1);
	cout << a[len-k];
}

P06. [算法课动态规划]走网格

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//棋盘
#include<iostream>
using namespace std;

int main() {
	int m, n;
	cin >> m >> n;
	int dp[11][11] = { 0 };
	dp[1][1] = 1;
	//初始化
	for (int i = 1; i <= m; i++) {
		for (int j = 1; j <= n; j++) {
			if (i == 1 || j == 1) {
				dp[i][j] = 1;
			}
			else {
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
			
		}
	}
	cout << dp[m][n];
	return 0;
}

P07. [算法课动态规划]爬楼梯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<iostream>

using namespace std;

int main() {
	int n;
	int dp[21];
	dp[0] = 1;
	dp[1] = 1;//零一阶都是只有一种方法达到
	cin >> n;
	for (int i = 2; i <= n; i++) {
		dp[i] = dp[i - 1] + dp[i - 2];
	}
	cout << dp[n];
	return 0;
}

P08. [算法课动态规划]背包问题

  • 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
  • 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//背包问题

#include<iostream>
using namespace std;

int main() {
	int weight[] = { 7,3,4,5 };
	int value[] = { 42,12,40,25 };
	int wetLen,cap;
	cin >> wetLen >> cap;
	int dp[11][11] = { 0 };
	for (int i = weight[0]; i <= cap; i++) {
		//能放物品1的进行初始化
		dp[0][i] = value[0];
	}
	//遍历物品
	for (int i = 1; i <= wetLen; i++) {
		//遍历背包容量
		for (int j = 1; j <= cap; j++) {
			if (j < weight[i-1]) dp[i][j] = dp[i - 1][j];//放不进，就是不妨上一个物品
			else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i-1]] + value[i-1]);//放的进就是比较上一个和放进这个的大小

		}
	}
	cout << dp[wetLen][cap];

	return 0;
}

P09 最长回文子串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/Problem P09. [算法课动态规划]最长回文子串

#include<iostream>
#include<string>
using namespace std;
int dp[1001][1001] = { 0 };
int main() {
	string s1;
	cin >> s1;
	
	//对角线为1
	for (int i = 0; i < s1.size(); i++) {
		for (int j = 0; j < s1.size(); j++) {
			if (i == j) {
				dp[i][j] = 1;
			}
		}
	}
	for (int i = s1.size()-1; i < s1.size(); i--) {
		for (int j = i ; j < s1.size(); j++) {
			//少了一个判断是两个字符的情况
			if (s1[i] == s1[j]) {
				//两个字符
				if (j - i <= 1) {
					dp[i][j] = 1;
				}
				else if (dp[i + 1][j - 1] == 1) {
					dp[i][j] = 1;
				}
			}
		}
	}
	//找最长的，记录下来
	int maxI = 0, maxJ = 0, maxdis = 0;
	for (int i = 0; i < s1.size(); i++) {
		for (int j = i; j < s1.size(); j++) {
			if (j - i > maxdis&&dp[i][j]==1) {
				maxI = i;
				maxJ = j;
				maxdis = j - i;
			}
		}
	}
	for (int z = maxI; z <= maxJ; z++) {
		cout << s1[z];
	}

	return 0;
}

P10 连续数组最大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//Problem P10.[算法课动态规划]连续数组最大和

#include<iostream>

using namespace std;
int main() {
	int n;
	int a[51] = { 0 };
	int dp[51][51] = { 0 };
	cin >> n;
	int p;
	for (int i = 0; i < n; i++) {
		cin >> p;
		a[i] = p;
	}
	for (int i = n - 1; i >= 0; i--) {
		for (int j = i; j < n; j++) {
			if (i == j) dp[i][j] = a[i];
			else dp[i][j] = dp[i + 1][j - 1] + a[i] + a[j];//加端点
		}
	}
	int max=0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (dp[i][j] > max) {
				max = dp[i][j];
			}
		}
	}
	cout << max;

	return 0;
}

⭐P11 最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<iostream>
#include<string>
using namespace std;
int dp[1001][1001] = { 0 };
int main() {
	string s1, s2;
	cin >> s1>>s2;
	//空出一个外围，非则会越界
	for (int i = 1; i <= s1.size(); i++) {
		for (int j = 1; j <= s2.size(); j++) {
            //注意i，i都要退一个
            //如果当前字母想都，就是左上角加上1
			if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
            //如果不同，找左边或者上边的最大值
			else {
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}
	cout << dp[s1.size()][s2.size()];
	return 0;
}

P12 贪婪 6和9组成的最大数字

简单跳过

P13 贪婪 三角形的最大周长

给定由一些正数（代表长度）组成的数组 A，返回由其中三个长度组成的、面积不为零的三角形的最大周长。如果不能形成任何面积不为零的三角形，返回 0。

  • 3 <= A.length <= 1000
  • 1 <= A[i] <= 1000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//Problem P13. [算法课贪婪]三角形的最大周长
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>

using namespace std;

int main() {
	int v;
	int a[1001] = { 0 };
	int count = 0;
	while (scanf("%d", &v) != EOF) {
		a[count] = v;
		count++;
	}
	//对a进行排序 冒泡排序 降序
	for (int i = 0; i < count; i++) {
		for (int j = 0; j < count - 1 - i; j++) {
			if (a[j] < a[j + 1]) {
				int temp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = temp;
			}
		}
	}
	int mark = 0;
	for (int i = 0; i + 3 <= count; i ++) {
		if (a[i + 1] + a[i + 2] > a[i] && a[i] - a[i + 1] < a[i + 2]) {
			cout << a[i] + a[i + 1] + a[i + 2];
			mark = 1;
			break;
		}
	}
	if (mark == 0) {
		cout << 0;
	}
	return 0;
}

用sort

1

P14 蛮力 种花问题

假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。

提示：

  • 1 <= flowerbed.length <= 2 * 10^4

  • flowerbed[i] 为 0 或 1

  • flowerbed 中不存在相邻的两朵花

  • 0 <= n <= flowerbed.length

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
//Problem P14.[算法课蛮力法]种花问题
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
int v[100001] = { 0 };
int main() {
	char a;

	int nums=0;
	int count = 0;
	while (scanf("%c", &a) != '\n') {
		if (a != ' ') {
			v[count] = a-'0';
			count++;
		}
		if (a == '\n') {
			break;
		}
		
	}
	cin >> nums;
	//nums=v[count-1];//最后一个就是插入总数
	count--;//去掉最后一个总数的
	/*cout << "nums:" << nums<<'\n';
	cout << "count:" << count << '\n'; cout << "v[count+1]:" << v[count+1] << '\n';*/
	//只有一个花坛
	if (nums <= 0) {
		cout << "true";
		return 0;
	}
	if (count == 1) {
		if (v[0] == 0 && nums == 1) {
			cout << "true";
			return 0;
		}
			
		
	}
	//第一个和最后一个特殊情况 先种最左和最右
	if (count >= 2) {
		if (v[0] == 0 && v[1] == 0) {
			nums--;
			v[0] = 1;
		}
		if ( v[count - 1] == 0 && v[count - 2] == 0) {
			nums--;
			v[count - 1] = 1;
		}
	}
	
	for (int i = 1; i < count-1; i++) {
		
		//开始从左往右有位置就种
		
		if (v[i - 1] == 0 && v[i + 1] == 0&&v[i]==0) {
			v[i] = 1; //种上后要赋值
			nums--;
		}
	}
	if (nums<=0) {
		cout << "true";
	}
	else {
		cout << "false";
	}
	//cout << '\n';
	/*for (int i = 0; i < count; i++)
		cout << v[i] << " ";*/
	//cout << '\n';
	//cout << "最后一个数" << v[count - 1] << '\n';
	// 真的猪啊，nums在前面经历过--操作，你在这里调试输出肯定对应不上原始值啊！！
	//cout << "转换到的最后一个" << nums << '\n';
	//cout << "总数" << count;
	return 0;
}

❗P15 贪婪 移掉K位数字(有一步没搞懂)

给你一个以字符串表示的非负整数 num 和一个整数 k ，移除这个数中的 k 位数字，使得剩下的数字最小。请你以字符串形式返回这个最小的数字。

  • 1 <= k <= num.length <= 1000
  • num 仅由若干位数字（0 - 9）组成
  • 除了 0 本身之外，num 不含任何前导零
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//
// Created by chan on 2023/12/13.
//
#include "bits/stdc++.h"
using namespace std;

int main(){
    int k=0;
    int count;
    string v;
    cin>>v>>k;

    //开始遍历
    for(int i=0;i<v.size();i++){
        while(k>0&&v.size()>0&&v[i]>v[i+1]){
            //前一个大于后一个
            v.erase(i,1);
            if(i>0) i--;
            k--;
        }
    }
    if(k>0&&v.size()){
        v.pop_back();
        k--;
    }
    //去除前导0
    int i=0;
    while(v[i]=='0'&&v.size()>0){
        v.erase(i,1);
    }
    if(v.size()==0){
        cout<<"0";
    }else{
        cout<<v;
    }

    return 0;
}

P16 贪婪 盛最多的水

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// Problem P16.[算法课贪婪]盛最多的水
// 思路从最远两边往里收缩，不是同时收缩，是一边一边收缩，记录最大
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<vector>
using namespace std;
int main() {
	//找第一长，和所有其他的算，再找第一二长和所有其他的算。。。
	char n;
	int len = 0;
	vector<int> v;
	int i;
	while (cin >> i) {
		v.push_back(i);
		if (cin.get() == '\n') break;
	}

	int l = 0,r=v.size()-1;
	int ans = 0, area = 0;
	while (l < r) {
		area = min(v[l], v[r]) * (r - l);//面积
		ans=max(ans,area);
		//小的一边收缩
		if (v[l] < v[r]) {
			l++;
		}
		else {
			r--;
		}
	}
	cout << ans;
	return 0;
}

P17 回溯 括号生成 void backTracking(int left, int right, string curstr)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//Problem P17.[算法课回溯]括号生成
#include<iostream>
#include<vector>
using namespace std;

int n;
vector<string> strs;//放string的数组
void backTracking(int left, int right, string curstr) {
	//递归结束条件
	if (right == 0 && left == 0) {
		strs.push_back(curstr);
		return;
	}
	//当剩余左边括号小于或等于右边时，才满足
	if (left <= right && left >= 0) {
		backTracking(left - 1, right, curstr + "(");//放左
		backTracking(left, right - 1, curstr + ")");//放右
	}
}
int main() {
	cin >> n;
	backTracking(n, n, "");
	cout << "[";
	for (int i = 0; i < strs.size(); i++) {
		cout << strs[i];
		if (i != strs.size() - 1) {
			cout << ", ";
		}
	}
	cout << "]";
	return 0;
}

P18 回溯 目标和 void check(int nums[], int tar, int n)

给你一个整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 ‘+’ 或 ‘-‘ ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-‘ ，然后串联起来得到表达式 “+2-1” 。 返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

提示：

  • 1 <= nums.length <= 20
  • 0 <= nums[i] <= 1000
  • 0 <= sum(nums[i]) <= 1000
  • -1000 <= target <= 1000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//
// Created by chan on 2023/12/13.
//
//Problem P18. [算法课回溯]目标和
#include<iostream>
using namespace std;


int count = 0;
int tsize = 0;
//数组 目标和 参与个数
void check(int nums[], int tar, int n) {
    if (tar == 0 && n == tsize) count++;
    if (n == tsize) return;//不满足但是退出
    check(nums, tar - nums[n], n + 1);
    check(nums, tar + nums[n], n + 1);
}




int main() {
    int nums[21];
    int target = 0;
    int a;
    int size=0;
    while (cin>>a)
    {
        nums[size] = a;
        size++;
        if (cin.get() == '\n') break;
    }
    cin >> target;
    tsize=size;
    check(nums,target,0);
    cout<<count;
    return 0;
}

P19 回溯 电话号码的字母组合 void backtracking(const string& s,int index,string curStr) 输入序列 序列号 可能组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案按字母顺序返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include<string>
#include <vector>
using namespace std;
//const char chara[][4]={{'a','b','c'},{'d','e','f'},{'g','h','i'},{'j','k','l'},{'m','n','o'},{'p','q','r','s'},{'t','u','v'},{'w','x','y','z'}};
const string chara[8] = {
        "abc", // 2
        "def", // 3
        "ghi", // 4
        "jkl", // 5
        "mno", // 6
        "pqrs", // 7
        "tuv", // 8
        "wxyz", // 9
};
vector<string> strs;
//标记当前是遍历到第几个
//_ _ x记录遍历到第几个，n记录第x个位置
void backtracking(const string& s,int index,string curStr){
    if(index==s.size()){//当这个满足时，说明前面的坑都填完了
        //三个位置都放好了
        strs.push_back(curStr);
        return;
    }
    int num=s[index]-'0'-2;//转为数值 取序号
    string letter=chara[num];
    for(int i=0;i<letter.size();i++){
        curStr.push_back(letter[i]);
        backtracking(s,index+1,curStr);//递归
        curStr.pop_back();//回溯
    }
}

vector<string> printPar(string s){
    if(s.size()==0){
        return strs;
    }
    backtracking(s,0,"");
    return strs;
}

int main() {
    //7,9长度是4，其他都是3
    string s1;
    cin>>s1;
    printPar(s1);
    cout<<"[";
    for(int i=0;i<strs.size();i++){
        cout<<strs[i];
        if(i<strs.size()-1) cout<<", ";
    }
    cout<<"]";
    return 0;
}

P20 回溯 优美的排列 void backtracking(int pos, int n) 位置数 长度

假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm（下标从 1 开始），只要满足下述条件 之一 ，该数组就是一个 优美的排列 ：

  • perm[i] 能够被 i 整除
  • i 能够被 perm[i] 整除

给你一个整数 n ，返回可以构造的 优美排列 的 数量 。

提示：

  • 1 <= n <= 15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//Problem P20. [算法课回溯]优美的排列
#include <iostream>
#include <string>
#include <vector>
using namespace std;
//int number[]={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
vector<int> vis=vector<int>(20,0);//标记作用
int res=0;
void backtracking(int pos, int n){
    if(pos>n) {
        res++;
    	return;
    }
    for(int i=1;i<=n;i++){
        if(vis[i]) continue;
        if(pos%i==0||i%pos==0){
            vis[i]=1;//访问
            backtracking(pos+1,n);
            vis[i]=0;//回溯
        }
    }

}

using namespace std;
int main(){
    //1-n所有排列的组合，边凑数，进行判断，如果不满足，置标记为false，直接排除当前情况
    int n;
    cin>>n;
    backtracking(1,n);
    cout<<res;
    return 0;
}

P21 组合 void backTracking(int n,int k,int startIndex) 长度 个数 遍历位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//
// Created by chan on 2023/11/8.
//
#include <iostream>
#include <vector>
using namespace std;
vector<int> path;
vector<vector<int>> result;
void backTracking(int n,int k,int startIndex){
    //n是氛围，k是个数，startIndex记录遍历到那个数了
    if(path.size()==k){//到叶子了，收割结果
        result.push_back(path);
        return;
    }
    for (int i = startIndex; i <=n ; ++i) {
        path.push_back(i);
        //递归
        backTracking(n,k,i+1);
        path.pop_back();//回溯
    }
}
int main(){
    int tar[21][21]={0};
    int n,k;
    cin>>n>>k;
    backTracking(n,k,1);
    for (int i = 0; i < result.size(); ++i) {
        for (int j = 0; j < result[i].size(); ++j) {
            cout<<result[i][j]<<" ";
        }
        cout<<'\n';
    }
    return 0;
}

P22 回溯 大礼包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
//
// Created by chan on 2023/11/8.
//
#include <iostream>
#include <vector>
using namespace std;
vector<int> goods;//商品即对应价格
vector<vector<int>> special;//存放大礼包
vector<int> need;//需要的各个商品数量

int specialn=0;//礼包种类数
int backTracking(vector<int> n){//n为need
    int ans=0;//此层决策要花多少钱
    for(int i=0;i<n.size();i++){
        ans+=goods[i]*n[i];//先不考虑买礼包
    }
    for (int i = 0; i < specialn; ++i) {//遍历礼包
        vector<int> tmp(n);//复制一遍需求，暂存
        int size_1bag=special[i].size();//礼包的大小
        int price=special[i][size_1bag-1];//存入礼包价格
        bool is_valid= true;//是否能买当前礼包
        for (int j = 0; j < size_1bag-1; ++j) {//遍历礼包的物品列表
            if(special[i][j]>n[j]){
                //有一个不满足
                is_valid= false;
                break;
            }
            tmp[j]-=special[i][j];//能买的话更新
        }
        if (is_valid){//能买礼包
            price+= backTracking(tmp);//当前礼包加上剩下需求所需的钱
            ans= min(ans,price);
        }else{//不能买礼包，换下一个
            continue;
        }
    }
    return ans;
}
int main(){
    //读取
    //
    // 假设有n个大礼包
    // 最基本的：一个大礼包都不买
    // 遍历所有大礼包包括自己（递归)
    /*
     * 终止条件：它加下一个礼包超出了数量
     * 首先大礼包的物品数要都小于目标数据
     * 不满足，则跳过，递归
     * 满足，则加入，算出总价，递归
     * 检查是否到最后一个大礼包
     *  是，判断还剩多少，用则用基本物品价格去补充
     * 问题:这里的k你不知道？即礼包的个数不定
     */
    vector<int> init;
    int n;
    while(cin>>n){
        init.push_back(n);
        if(cin.get()=='\n') break;
    }
    //前size-1都是商品
    for (int i = 0; i < init.size()-1; ++i) {
        goods.push_back(init[i]);
    }
    int speciallen=init[init.size()-1];

    for(int i=0;i<speciallen;i++){
        vector<int> save;
        for(int j=0;j<goods.size()+1;j++){
            cin>>n;
            save.push_back(n);
        }
        special.push_back(save);
    }
    for(int i=0;i<goods.size();i++){
        cin>>n;
        need.push_back(n);
    }

    specialn=special.size();

    cout<< backTracking(need);
    return 0;
}

P23 计数排序

image-20231212144444548

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//
// Created by chan on 2023/11/15.
// 计数排序
#include <iostream>
using namespace std;
#define N 10000000
int a[N],b[N],c[N]={0};
int n=0,m=0,bi=0;
int mod=1e9+7;
long long ans;
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i){
        scanf("%d",&a[i]);
        ++c[a[i]]; //这里按序号赋值，本身就已经有序了，不用排序了
    }
    for(int i=1;i<=m;++i){
        for(int j=1;j<=c[i];++j){
            b[++bi]=i;//重复的a[i]进行排序 0的话自动跳过了巧妙
        }
    }
    for(int i=1;i<=n;++i){
        (ans+=1LL*i*b[i])%=mod;
    }
    printf("%lld\n",ans);
    return 0;

}

P24 贪心 跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度

判断你是否能够到达最后一个下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
using namespace std;
int num[100001]={0};
int main(){
    int a;
    int size=0;
    while(cin>>a){
        num[size]=a;
        size++;
        if(cin.get()=='\n') break;
    }
    int latTar=0;//上一个0
    int curTar=0;//标记当前出现0的位置
    bool flag=true;//能到最后的标记
    if (num[0]==0){
        cout<<"false";
        return 0;
    }
    for(int i=0;i<size;i++){
        if(num[i]==0){
            curTar=i;
            bool canFly= false;
            //查到0，判断前面有没有能够跳过0的
            for(int j=i-1;j>=latTar;j--){
                if(j+num[j]>curTar){
                    canFly= true;
                }
            }
            if(!canFly){
                flag=false;
                break;
            }
        }
    }
    if(flag) cout<<"true";
    else cout<<"false";
    return 0;
}

法2

维护一个可达到的最远位置maxPos，通过遍历当前可跳跃范围内的所有位置，计算每个位置能够达到的最远位置，并更新maxPos。如果maxPos超过数组长度的最后一个位置，则表示可以到达末尾，返回true；否则，根据当前位置调整下一次可跳跃范围的起点和终点，直到无法继续跳跃返回false。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int main(){
    int a;
    vector<int> v;
    while(cin>>a){
        v.push_back(a);
        if(cin.get()=='\n') break;
    }
    int maxPos=0,left=0,right=0,flag=0;
    while(left<=right){
        if(maxPos>=v.size()-1){
            flag=1;
            break;
        }
        for(int i=left;i<=right;i++){

            maxPos=max(maxPos,i+v[i]);
        }
        left=right+1;
        right=maxPos;
    }
    if (flag) cout<<"true";
    else cout<<"false";

    return 0;
}

P25 动规 整数拆分

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。

我们用dp[i]来表示分拆数字i，可以得到的最大乘积，对于每个i来说，都可以通过前面已知的拆分结果来求，遍历i前面的每个数字j，假设拆分成两个数 j 和 i-j ，这是一种情况，另外，j 又可以继续拆分，j拆分的最大值就是dp[j]， 同理 i-j 也是一样的，我们在所有情况里取最大值就是dp[i]的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//
// Created by chan on 2023/11/26.
//

#include "iostream"
using namespace std;

int main(){
    int n;
    int dp[60]={0};
    cin>>n;
    dp[1]=1;
    dp[2]=1;
    if(n<=2) {
        cout<<dp[n];
        return 0;
    }
    for(int i=3;i<=n;i++){
        for(int j=1;j<i-1;j++){
            dp[i]=max(dp[i], max(j*(i-j),dp[i-j]*j));
        }
    }
    cout<<dp[n];

    return 0;
}

P26 动态规划 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

提示：

  • 1 <= nums.length <= 100
  • 0 <= nums[i] <= 400
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Problem P26. [算法课动态规划] 打家劫舍
#include "iostream"
#include "vector"
using namespace std;
int main(){
    vector<int> room;
    room.push_back(0);//占着第0个
    int n;
    int dp[101]={0};
    while(cin>>n){
        room.push_back(n);
        if(cin.get()=='\n') break;
    }
    dp[1]=room[1];
    //初始化dp
    //遍历dp
    for(int i=2;i<=room.size()-1;i++){
        dp[i]=max(dp[i-1],dp[i-2]+room[i]);//不偷本间,偷本间加前面的第二间
    }
//    cout<<room.size()<<endl;
    cout<<dp[room.size()-1];
    return 0;
}

P27 动态规划 戳气球

image-20231212145315276

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
// Problem P27. [算法课动态规划] 戳气球
#include "iostream"
#include <math.h>
#include "vector"

using namespace std;
int maxCoins(vector<int> nums){
    int n = nums.size();
    // 添加两侧的虚拟气球
    vector<int> points(n+2) ;//= new int[n + 2]
    points[0] = points[n + 1] = 1;
    for (int i = 1; i <= n; i++) {
        points[i] = nums[i - 1];//nums从0开始
    }
    // base case 已经都被初始化为 0
    vector<vector<int>>dp(n+2,vector<int>(n+2));//    int[][] dp = new int[n + 2][n + 2];

    // 开始状态转移
    // i 应该从下往上
    for (int i = n; i >= 0; i--) {
        // j 应该从左往右
        for (int j = i + 1; j < n + 2; j++) {
            // 最后戳破的气球是哪个？
            for (int k = i + 1; k < j; k++) {
                // 择优做选择
                dp[i][j] = max(
                        dp[i][j],
                        dp[i][k] + dp[k][j] + points[i]*points[j]*points[k]
                );
            }
        }
    }
    return dp[0][n + 1];
}
int main(){
    vector<int> nums;
    int n;
    while (cin>>n){
        nums.push_back(n);
        if(cin.get()=='\n') break;
    }
    cout<<maxCoins(nums);


    return 0;
}

P28 贪心 跳跃游戏

有一个非负整数数组 nums，最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

假设你总是可以到达数组的最后一个位置, 你的目标是使用最少的跳跃次数到达数组的最后一个位置。

输入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//
// Created by chan on 2023/11/22.
//
#include "iostream"
#include "vector"
using namespace std;


/*
 * 基本思想
 * 每次在当前能跳跃范围内选择可以使得接下来能跳跃最远的位置
 */
vector<int> nums;

int findMaxStep(vector<int> vector1);

int main(){
    int n;
    int a;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a;
        nums.push_back(a);
    }
    cout<<findMaxStep(nums);
}

int findMaxStep(vector<int> vector1) {
    int maxReach=0;//记录跳到最远的
    int curReach=0;
    int cnt=0;
    int maxPos=0;
    while (curReach<=maxReach&&maxPos<vector1.size()-1){
        cnt++;
//        curReach=maxReach;//当前的位置
//        maxReach=vector1[curReach]+curReach;//首先初始化一个最远
        for(int i=curReach;i<=maxReach;i++){
            //跳得超越了之前的maxReach
            maxPos= max(maxPos,i+nums[i]);
        }
        curReach=maxReach+1;
        maxReach=maxPos;
    }

    return cnt;
}

P29 指针 颜色分类

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

输入

第一行输入一个整数 n (1≤n≤300)n (1≤n≤300) 代表数组的长度。

第二行输入一行数字代表数组 nums[i] 为0，1，2，数字与数字之间用空格间开。

输出

输出排序后的数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
//Problem P29. [算法课指针] 颜色分类

#include <iostream>
using namespace std;
int key[3]={0};//检查三种颜色
void sortColor(int *head,int n){
    if(n==1) return;
    int *p= nullptr;//工作指针
    int *edge= head;
    int *hh=head;
    int temp=-1;
    for(int i=0;i<3;i++){
        //检查head
        head=edge;
        p=head;

        while (*p!=i&&*p!=-1) p++;//找到颜色头一个
        if(*p==-1) continue;
        temp=*p;
        *p=*head;
        *head=temp;
        key[i]=1;//头部解决，建议记录头部索引
        edge=head;//存储颜色族头
        head++;
        while(*head!= -1){
            //进入一个聚类的循环

            p=head;
            while(*p!=i&&*p!=-1) {
                p++;
            }
            //找到一个替换
            if(*p==-1) {
                edge=head;
                break;
            }
            temp=*p;
            *p=*head;
            *head=temp;
            //直到越界
            head++;
        }
    }
}
int main(){
    int n;
    int nums[301]={0};
    int a;
    for(int i=0;i<301;i++) nums[i]=-1;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a;
        nums[i]=a;
    }
    sortColor(nums,n);
    cout<<'[';
    for(int i=0;i<n-1;i++) cout<<nums[i]<<",";
    cout<<nums[n-1]<<']';
    return 0;
}